一文读懂向量数据库

一、GPT的缺陷

🔥 最近一年的时间里，我们正处于人工智能革命的浪潮中，以ChatGPT为代表的大语言模型横空出世，带给我们无限震撼的同时，其天然的缺陷和诸多的限制也让开发者头痛不已，如输入上下文token的限制、不具备记忆能力等等。

😨 这种情况有点类似于早期开发者面对内存只有几MB甚至几KB时期开发应用的窘境，一是“内存”昂贵，二是“内存”太小，所以GPT模型在性能、成本、注意力机制等方面有重大革命性进展前，开发者不得不面临如何解决GPT tokens限制的问题。

二、向量数据库介绍

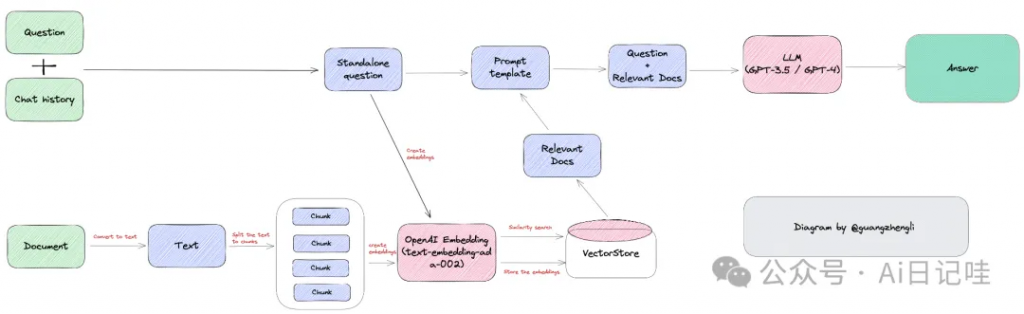
🤔 在GPT模型限制的情况下，开发者们不得不寻找其他解决方案，向量数据库就是其中之一。

✍️ 向量数据库的核心是将文本转换为向量，然后存储在向量数据库中，当用户输入问题的时候，将问题也转化为向量，在向量数据库中查找最相似的上下文向量，最终将文本返回给用户。

👀 举个例子：

1️⃣ 当我们有一份文档需要GPT处理时，假设这份文档是客服培训资料或操作手册，我们可以先将这份文档的所有内容转化为向量，并存储到向量数据库中。然后当用户提出相关问题时，我们将用户的搜索内容转换为向量，在向量数据库中搜索最相似的上下文向量，返回给GPT。这样不仅可以大大减少GPT的计算量，从而提高响应速度，更重要的是降低成本，并绕过GPT的tokens限制。

👀 再举个例子：

2️⃣ 当我们和ChatGPT之间有一段很长的对话，我们可以将过去的对话以向量的方式保存起来，当我们提问给ChatGPT时，将问题转化为向量，对过去所有的聊天记录进行语义搜索，找到与当前问题最相关的“记忆”，一起发送给ChatGPT，极大提高ChatGPT的输出质量。

三、向量数据库的技术原理

3.1 词嵌入技术（Embeding）

👱♂️ 传统数据库一般都是通过不同的索引方式（B Tree、倒排索引）加上关键词匹配等方法实现的，本质上还是基于文本的精确匹配，语义搜索的功能较弱。

😐 比如，搜索”小狗”，只能得到带有”小狗”关键词的结果，而无法得到”柴犬”、”哈士奇”等结果。因为”小狗”和”柴犬”是不同的关键词，传统数据库无法识别他们的语义关系。

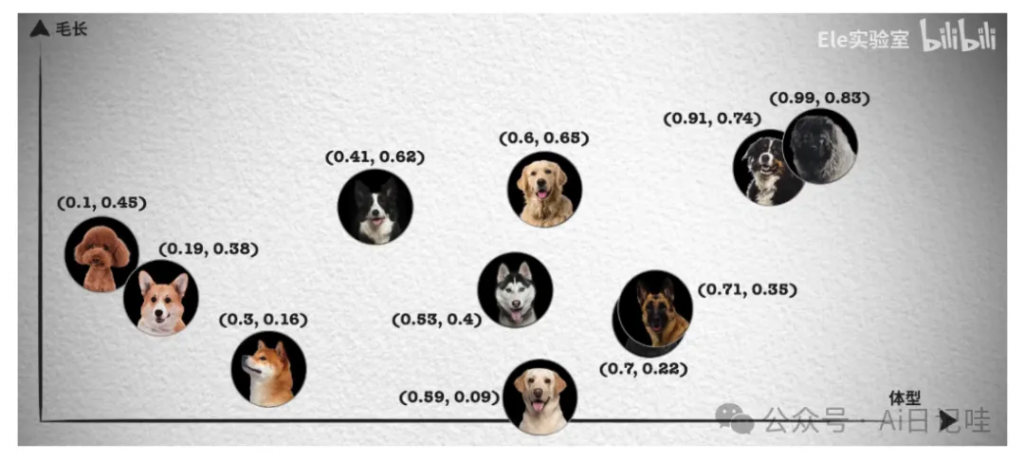
🤔 我们可以使用模型提取不同关键词的特征，得到特征向量，不同向量之间可以通过内积或余弦来判断其相似性关系，这样便可以使用特征向量进行语义搜索。将关键词转换为特征向量的过程，被称为Embeding。

3.2 相似性搜索（HNSW）

🤔 我们已经知道可以通过比较向量之间的距离来判断他们的相似度，那么如何将其应用到真实的场景中呢？

🛠️ 如果想要在海量的数据中找到和某个向量最相似的向量，我们需要对数据库中的每个向量都进行一次比较计算，但这样的计算量是非常巨大的，所以我们需要一种高效的算法来解决这个问题。

⚱️ 目前业界主流的方法是通过构建图的方式来实现最近邻搜索，比较有名的HNSW算法是一种基于图的近似最近邻搜索（Approximate Nearest Neighbor Search）算法，主要用于在极大量的候选集中快速找到与查询点（query）最近邻的k个元素。

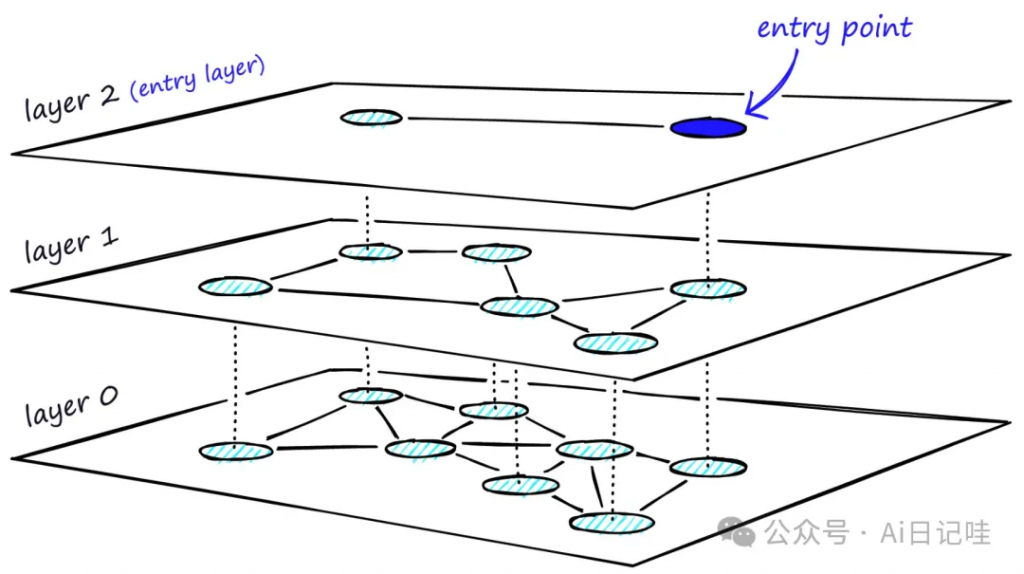
📡 算法步骤如下：

1️⃣ 构建索引
- 随机选取初始点：从数据集中随机选取一个点作为初始点。
- 逐层构建超平面：依次将其他点插入到合适的层中，并为每个点分配一个层号，表示该点在哪一层中。
2️⃣ 在索引中查找最近邻
- 从顶层开始搜索：给定一个查询点，从最顶层开始逐层向下搜索。
- 确定最近邻：通过计算余弦相似度或距离来确定离查询点最近的点。
- 加速搜索：在搜索过程中，可以采用剪枝和优先队列等技术来加速搜索过程。

💻 算法特点：

1️⃣ 高效性：通过构建多层的超平面，将高维空间中的数据点组织成一个层次化的结构，使得查找最近邻的时间复杂度降低至O(log n)。
2️⃣ 近似性：采用小世界图的结构，使得搜索结果具有一定的近似性。虽然不能保证找到的最近邻一定是真实最近邻，但可以通过调整参数来控制近似程度和搜索性能的平衡。
3️⃣ 可扩展性：HNSW算法可以很容易地支持新增数据点和删除数据点，同时也可以支持高维空间的搜索。

3.3 距离度量

🙋♂️ 上面我们讨论了向量数据库的不同搜索算法，但是还没有讨论如何衡量相似性。在相似性搜索中，需要计算两个向量之间的距离，然后根据距离来判断它们的相似度。

🔎 而如何计算向量在高维空间的距离呢？有三种常见的向量相似度算法：

欧几里德距离
余弦相似度
点积相似度

📕 下面分别介绍这三种距离度量方式：

1️⃣ 欧氏距离

欧几里得距离是指两个向量之间的距离，它的计算公式为：

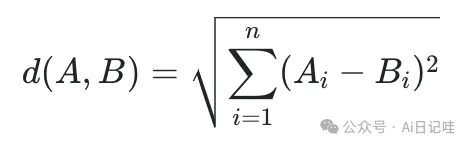
👓 其中，A和B分别表示两个向量，n表示向量的维度。

🎒 欧几里得距离算法的优点是可以反映向量的绝对距离，适用于需要考虑向量长度的相似性计算。例如推荐系统中，需要根据用户的历史行为来推荐相似的商品，这时就需要考虑用户的历史行为的数量，而不仅仅是用户的历史行为的相似度。

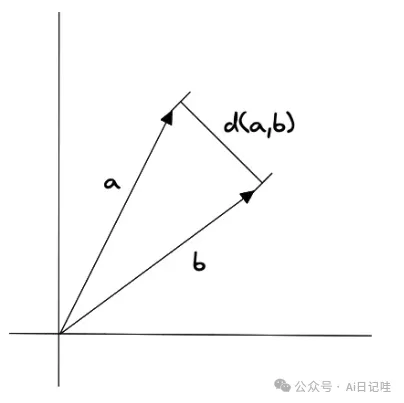
2️⃣ 余弦相似度

余弦相似度是指两个向量之间的夹角余弦值，它的计算公式为：

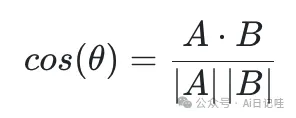
👓 其中，A和B分别表示两个向量，·表示向量的点积，|A|和|B|分别表示两个向量的模长。

🎒 余弦相似度对向量的长度不敏感，只关注向量的方向，因此适用于高维向量的相似性计算。例如语义搜索和文档分类。将归一化后的向量进行点积，实际上也是余弦相似度。

3️⃣ 点积

向量的点积相似度是指两个向量之间的点积值，它的计算公式为：

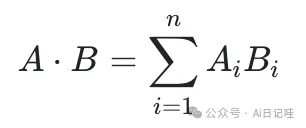
👓 其中，A和B分别表示两个向量，n表示向量的维度

🎒 点积相似度算法的优点在于它简单易懂，计算速度快，并且兼顾了向量的长度和方向。它适用于许多实际场景，例如图像识别、语义搜索和文档分类等。但点积相似度算法对向量的长度敏感，因此在计算高维向量的相似性时可能会出现问题。

🙋♂️ 每一种相似性测量 (Similarity Measurement) 算法都有其优点和缺点，需要开发者根据自己的数据特征和业务场景来选择。

四、总结

👨🎓 本文主要介绍了向量数据库的原理和实现，包括向量数据库的基本概念、相似性搜索算法、相似性测量算法。向量数据库是崭新的领域，目前大部分向量数据库公司的估值乘着 AI 和 GPT 的东风从而飞速的增长，但是在实际的业务场景中，目前向量数据库的应用场景还比较少，抛开浮躁的外衣，向量数据库的应用场景还需要开发者们和业务专家们去挖掘。

文章转自微信公众号@Ai日记哇