方差公式：从定义到应用详解

在统计学与概率论中，方差是一个重要的概念，用于度量数据集中各个值偏离平均值的程度。本文将深入探讨方差公式的定义、性质及其在不同概率分布中的应用。

1. 方差的定义与重要性

方差是随机变量与其均值之间偏离程度的度量工具。具体来说，方差被定义为随机变量与其期望值之差的平方的期望值，用公式表示为：

[ D(X) = E[(X – E(X))^2] ]

在实际应用中，方差帮助我们理解数据的分散程度。例如，在评估生产线灯泡寿命时，仅仅知道平均寿命并不够，方差可以揭示寿命的波动情况。

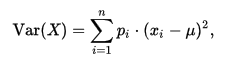
2. 方差的基本性质

方差具有以下几个基本性质：

方差为零：当且仅当随机变量是常数时，即所有观测值都相同。
方差的线性性质：对于常数 ( C ) 和随机变量 ( X )，有 ( D(CX) = C^2D(X) ) 和 ( D(X + C) = D(X) )。
独立性：若两个随机变量 ( X ) 和 ( Y ) 相互独立，则 ( D(X+Y) = D(X) + D(Y) )。

3. 常见分布的方差

在统计学中，不同类型的分布有各自的方差公式。以下是几个常见分布的方差：

3.1 (0-1) 分布

(0-1) 分布又称为伯努利分布，其方差公式为：

[ D(X) = p(1-p) ]

其中，( p ) 是事件发生的概率。此分布用于描述单次实验的成功或失败，如抛硬币。

3.2 二项分布

二项分布是多次独立伯努利试验的结果，其方差为：

[ D(X) = np(1-p) ]

其中，( n ) 是试验次数，( p ) 是成功的概率。二项分布常用于描述多个相同实验的总成功次数。

3.3 泊松分布

泊松分布用于描述一定时间内随机事件发生的次数，其方差为：

[ D(X) = lambda ]

这里，( lambda ) 是单位时间内事件发生的平均次数。泊松分布广泛应用于排队论和库存管理。

3.4 几何分布

几何分布用于描述第一次成功前的失败次数，其方差为：

[ D(X) = \frac{1-p}{p^2} ]

几何分布在模拟游戏或金融中风险分析中应用广泛。

3.5 超几何分布

超几何分布用于描述从有限总体中不放回抽样成功的次数，其方差为：

[ D(X) = n\frac{M}{N}(1-\frac{M}{N})(\frac{N-n}{N-1}) ]

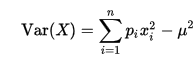
4. 方差在数据分析中的应用

方差不仅是理论上的度量工具，在实际数据分析中也至关重要。通过方差，我们可以判断数据的波动性，识别异常值，并在机器学习中用于特征工程和模型评估。

5. 方差与标准差的关系

标准差是方差的平方根，提供了与原数据相同单位的波动性度量，便于解释和比较不同数据集。标准差公式为：

[ sigma(X) = sqrt{D(X)} ]

6. 方差的计算方法

在实际计算中，方差常通过以下公式计算：

[ D(X) = E(X^2) – [E(X)]^2 ]

这一公式便于简化计算过程，尤其是对于大数据集。

7. 方差的可视化

通过图形化手段，如盒须图或直方图，我们可以直观展示数据的方差和分布情况。图形化展示有助于更好地理解数据特征和做出决策。

FAQ

问：方差和标准差有什么区别？
- 答：方差表示数据的离散程度，其单位是原数据单位的平方；标准差是方差的平方根，与原数据单位相同。
问：方差可以为负数吗？
- 答：不可以，方差是平方项的平均值，因此总是非负数。
问：如何使用 Python 计算方差？
- 答：可以使用 Python 的 numpy 库中的 var() 函数来计算数组的方差。

本文通过详尽的分析和证明，揭示了方差公式在统计学中的重要性及其广泛应用。通过理解不同分布的方差公式，我们可以更好地应用统计工具进行数据分析和决策。

方差公式：从定义到应用详解