方差分析（ANOVA）详解与应用

方差分析（Analysis of Variance，简称ANOVA）是统计学中用于比较三个或以上样本均值差异的强有力工具。本文将详细介绍方差分析的基本原理、计算方法、R语言实现以及结果解读，并通过图表和代码示例增强理解。

一、方差分析的基本原理

1.1 主效应与交互效应

方差分析通过分析各变量的主效应和交互效应，帮助我们发现因变量的变异来源。主效应指的是单个因素对因变量的影响，而交互效应则涉及多个因素共同作用于因变量的结果。

1.2 实验设计与数据获取

实验设计中，通过对研究对象进行不同处理，并控制各变量的水平，我们可以观察到实验对象某一指标（因变量）在不同实验单位间的差异。

实验设计示意图

1.3 数学模型与方差分解

方差分析的基本思路是将数据的变异划分为组内变异和组间变异，并通过F检验比较二者差异的显著性。

data <- data.frame(

  Treatment = rep(c("A", "B", "C"), each = 5),

  Value = c(12, 15, 14, 13, 16, 10, 11, 13, 12, 14, 15, 14, 13, 15, 16, 17, 14)

)

二、方差分析的计算方法

2.1 方差分解

在方差分析中，方差通过平方和与自由度来计算，将总变异分解为组间变异和组内变异。

2.2 组间与组内平方和

组间平方和（SSB）和组内平方和（SSW）的计算是方差分析的关键步骤。

SSB <- sum((data$Value[1:5] - mean(data$Value[1:5]))^2 +

               (data$Value[6:10] - mean(data$Value[6:10]))^2 +

               (data$Value[11:15] - mean(data$Value[11:15]))^2)

SSW <- sum((data$Value[1:5] - mean(data$Value))^2 +

               (data$Value[6:10] - mean(data$Value))^2 +

               (data$Value[11:15] - mean(data$Value))^2)

2.3 自由度的计算

自由度（df）是方差分析中另一个重要的概念，它与平方和紧密相关。

三、R语言实现方差分析

3.1 R语言中的方差分析

R语言提供了强大的包来执行方差分析，如stats包。

fit <- aov(Value ~ Treatment, data = data)

summary(fit)

3.2 结果解读

方差分析的结果通常包括F统计量和P值，用于判断处理效应是否显著。

四、方差分析的图表展示

4.1 箱型图的应用

箱型图是展示方差分析结果的常用图表，它能有效展示数据分布和处理效应的显著性。

library(ggplot2)

ggplot(data, aes(x = Treatment, y = Value)) +

  geom_boxplot() +

  labs(title = "Boxplot of Treatment Effects", x = "Treatment", y = "Value")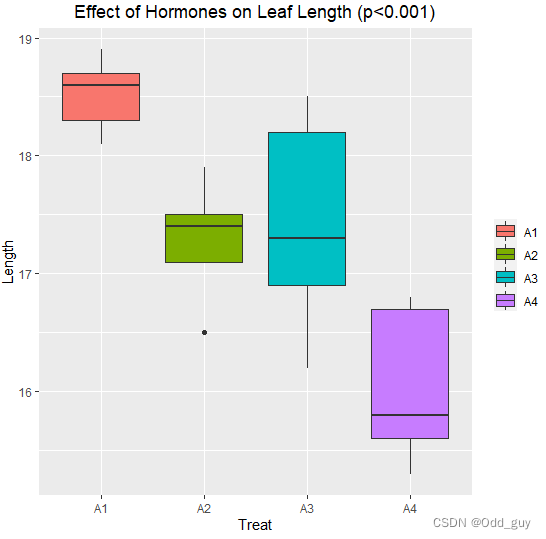

箱型图示例

4.2 多重比较测试

多重比较测试用于进一步分析不同处理组之间的差异。

FAQ

问：方差分析中的自由度是如何计算的？
- 答：自由度（df）是组内或组间数据点数减去组数得到的。例如，组间自由度为组数减1，组内自由度为总样本数减去组数。
问：F统计量的意义是什么？
- 答：F统计量用于比较组间变异与组内变异的大小，其值越大，表明组间差异越显著。
问：如何解释P值？
- 答：P值用于判断统计结果的显著性。P值小于0.05通常表示结果具有统计显著性。
问：箱型图在方差分析中的作用是什么？
- 答：箱型图能够直观展示不同处理组的数据分布情况，包括中位数、四分位数和异常值，帮助识别数据中的异常和差异。
问：多重比较测试有哪些常用方法？
- 答：常用多重比较测试方法包括LSD测试、Tukey测试、Bonferroni测试等，它们用于进一步分析不同处理组之间的具体差异。