拓扑空间：定义与应用

拓扑空间是数学中一个重要的概念，广泛应用于现代数学的许多分支。本文将深入探讨拓扑空间的基本定义、特性以及其在不同领域的应用。

拓扑空间的定义

集合与邻域

拓扑空间可以被定义为一个包含点的集合，与每个点的邻域集合相关，满足特定的公理。一个拓扑空间的基本定义通常涉及集合、点和邻域。具体来说，拓扑空间由一个集合 $X$ 和一个称为拓扑的集合 $ au$ 组成，其中 $ au$ 是 $X$ 的子集的集合，满足以下公理：

空集和 $X$ 本身都属于 $ au$。
$ au$ 中任意元素的并集属于 $ au$。
$ au$ 中任意有限个元素的交集属于 $ au$。

这些公理确保了拓扑空间的基本结构和性质。

示例图1

开集定义

拓扑空间的另一种常见定义是通过开集（open sets）。在这种定义中，一个拓扑空间由一个二元组 $(X, au)$ 构成，其中 $X$ 是非空集合，$ au$ 是 $X$ 的子集的集合，且满足如下性质：

空集和 $X$ 属于 $ au$。
$ au$ 中任意数量的并集属于 $ au$。
$ au$ 中任意有限数量的交集属于 $ au$。

通过开集的定义，我们可以更直观地理解拓扑空间的结构。

示例图2

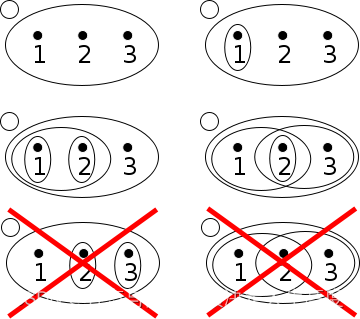
拓扑空间的性质

邻域性质

拓扑空间中的邻域是指包含某个点的一个开集。根据定义，拓扑空间中的邻域具有以下特性：

任意两个邻域的交集仍然是一个邻域。
包含一个邻域的集合也是一个邻域。
一个邻域的内点集合也是一个邻域。

这些性质帮助我们理解拓扑空间中点与邻域之间的关系。

通过集合构造拓扑

在数学中，我们常常通过集合构造拓扑。例如，假设 $X = {1, 2, 3}$，我们可以构造出不同的拓扑，如：

$tau_1 = {emptyset, X, {1, 2}, {2, 3}}$
$tau_2 = {emptyset, X, {1}, {1, 2, 3}}$

每个拓扑都满足基本的拓扑公理，但其结构可能大不相同。

拓扑空间的应用

在数学中的应用

拓扑空间在数学的多个领域中扮演着重要角色。它不仅是分析学、几何学的重要工具，还涉及到代数拓扑和微分拓扑等领域。在这些领域中，拓扑空间帮助我们研究空间的连续性和变换。

在物理中的应用

物理学中，拓扑空间常用于研究宇宙的结构和物质的性质。例如，在量子场论中，拓扑空间帮助我们理解粒子的相互作用和对称性。

在计算机科学中的应用

拓扑空间的概念也被引入到计算机科学中，特别是在数据分析和机器学习领域。在这些领域中，拓扑空间用于处理数据的几何结构和高维数据的映射。

通过示例理解拓扑空间

示例1：三元素集合的拓扑

考虑集合 $X = {a, b, c}$，我们可以定义一个拓扑 $tau = {emptyset, X, {a, b}, {b, c}}$。此拓扑满足所有拓扑公理：

空集和 $X$ 包含于 $tau$。
${a, b}$ 和 ${b, c}$ 的并集 ${a, b, c}$ 属于 $tau$。
${a, b}$ 和 ${b, c}$ 的交集 ${b}$ 不属于 $tau$，但这不影响 $tau$ 的有效性，因为交集不一定需要是 $tau$ 的成员。

示例2：开集的应用

假设我们有一个集合 $Y = {1, 2, 3, 4}$，定义拓扑为 $sigma = {emptyset, Y, {1, 2}, {3, 4}}$。这是一个合法的拓扑，因为：

空集和 $Y$ 属于 $sigma$。
任意元素的并集属于 $sigma$，如 ${1, 2} cup {3, 4} = Y$。
任意有限个元素的交集也属于 $sigma$，如 ${1, 2} cap {3, 4} = emptyset$。

拓扑空间的相关问题

FAQ

问：什么是拓扑空间的基本要素？
- 答：拓扑空间的基本要素包括一个集合及其上的拓扑结构，即满足特定公理的子集集合。
问：拓扑空间如何应用于计算机科学？
- 答：在计算机科学中，拓扑空间用于分析数据结构、优化算法和研究高维数据集的几何特性。
问：拓扑空间与向量空间有何区别？
- 答：拓扑空间关注空间的连续性和邻域关系，而向量空间专注于线性结构和代数运算。
问：如何通过例子理解拓扑空间？
- 答：通过简单集合的拓扑结构分析和应用，可以更直观地理解拓扑空间的性质和作用。
问：拓扑空间在物理学中有何应用？
- 答：拓扑空间在物理学中用于研究宇宙结构、量子场论中的粒子相互作用及材料科学中的物质性质。

通过本文的探讨，我们了解了拓扑空间的基本概念、特性以及其在数学、物理和计算机科学中的广泛应用。拓扑空间不仅是一个数学定义，更是理解复杂系统和结构的重要工具。