时间序列分析与预测：从基础到应用

时间序列分析是一种强大而灵活的工具，用于理解和预测按时间顺序排列的数据。无论是在金融市场中的股票价格预测，还是在气候研究中的温度变化分析，时间序列的应用广泛而深入。本文将详细探讨时间序列的定义、组成部分、预测方法以及在实际应用中的技巧和挑战。

什么是时间序列？

时间序列是一组按照时间顺序排列的数据点。这些数据点可以代表各种现象，例如每小时的气压、每年的医院急诊、按分钟计算的股票价格等。时间序列的关键在于其时间维度，这使得分析和预测不仅仅关注数据点本身，还要考虑其随时间的变化。

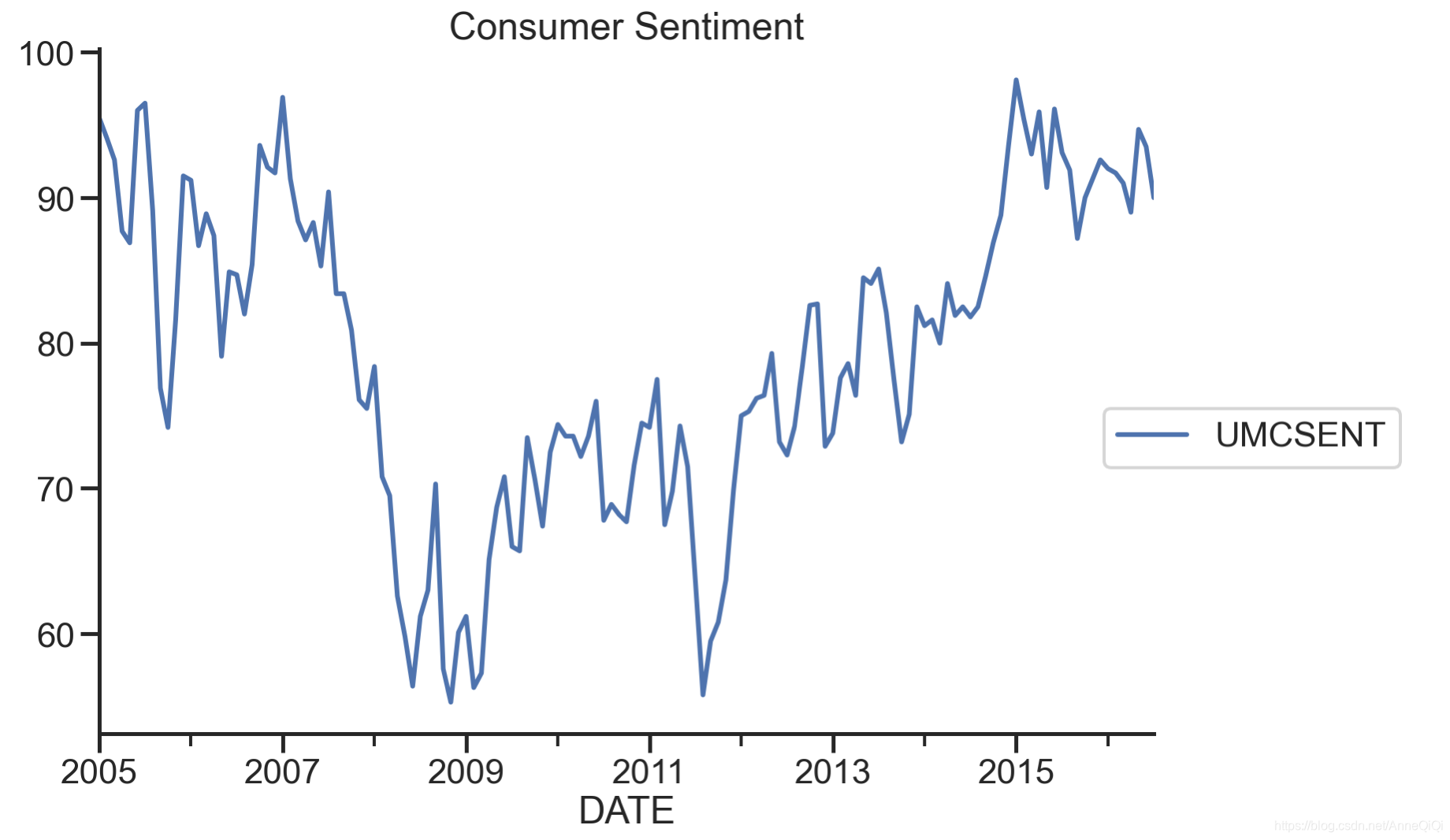
时间序列示例

时间序列数据的特征

时间序列数据的一个显著特征是其数据点是相互关联的，且这种关联是随时间推进的。这意味着在分析时间序列时，需要关注数据点之间的时间依赖性，而不仅仅是每个数据点的数值。

时间序列的组成部分

时间序列数据通常由多个组成部分构成：趋势、季节性、循环性和残差或白噪声。

趋势

趋势是指时间序列中长期的、缓慢变化的方向。趋势可以是上升的、下降的，或是保持稳定的。在时间序列分析中，识别趋势有助于理解数据的总体方向性。

趋势示例

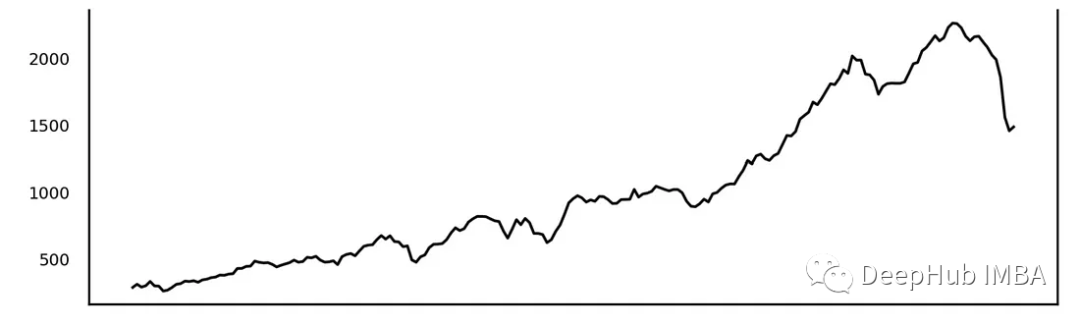
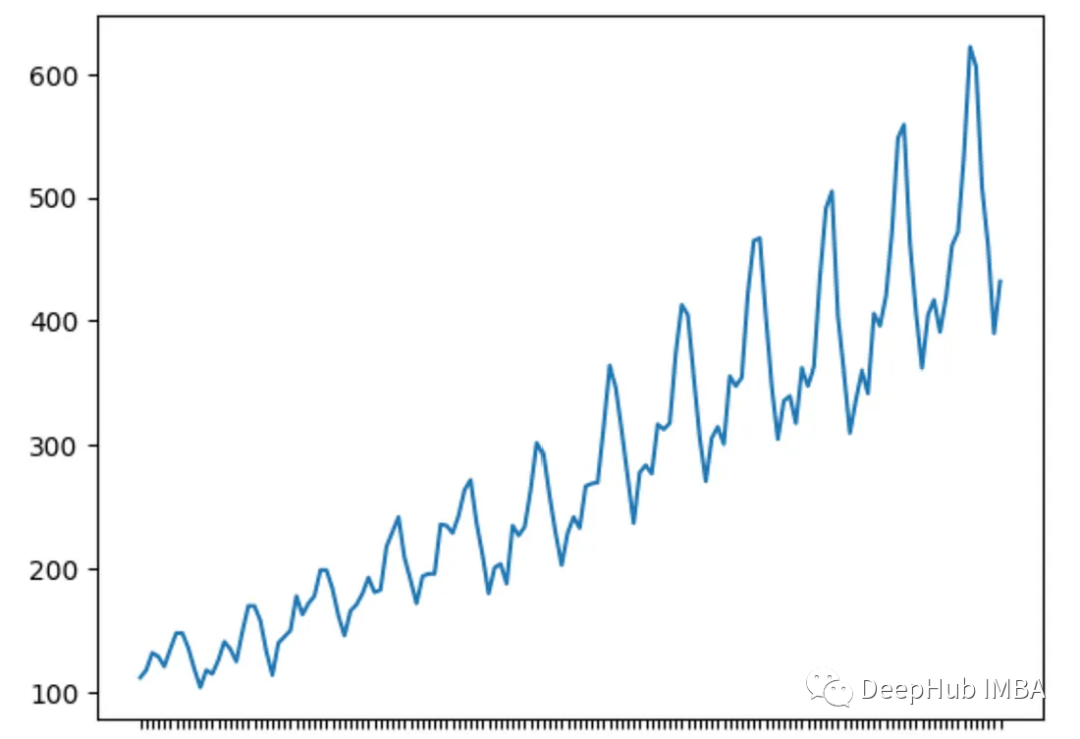
季节性

季节性是指在固定时间间隔内重复出现的模式。这种模式通常与季节、时间或其他周期性因素有关。识别季节性模式可以帮助预测未来的变化。

季节性示例

残差或白噪声

残差或白噪声是指时间序列中无法用趋势或季节性解释的随机模式。这些随机性因素可能会影响数据的准确性，因此在分析时需要特别注意。

残差示例

时间序列分解与建模

时间序列分解是将时间序列数据分解为其组成部分的过程。通过分解，分析人员可以更清晰地理解每个成分的作用，从而提高预测的准确性。

时间序列分解

我们可以使用 Python 中的 statsmodels 库来分解时间序列。以下是一个简单的代码示例：

import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import STL

df = pd.read_csv("time-series-data.csv")

decomposition = STL(df['x'], period=12).fit()

fig, (ax1, ax2, ax3, ax4) = plt.subplots(nrows=4, ncols=1, sharex=True, figsize=(10, 8))

ax1.plot(decomposition.observed)
ax1.set_ylabel('Observed')

ax2.plot(decomposition.trend)
ax2.set_ylabel('Trend')

ax3.plot(decomposition.seasonal)
ax3.set_ylabel('Seasonal')

ax4.plot(decomposition.resid)
ax4.set_ylabel('Residuals')

plt.tight_layout()
plt.show()

时间序列预测模型

在进行时间序列预测时，常用的模型包括：

自回归(AR)模型
移动平均(MA)模型
自回归移动平均(ARMA)模型
自回归综合移动平均(ARIMA)模型
季节自回归综合移动平均(SARIMA)模型
带有外源回归量的季节自回归综合移动平均(SARIMAX)模型

对于大数据集，深度学习模型如多层感知器(MLP)、循环神经网络(RNN)和长短期记忆网络(LSTM)也被广泛使用。

预测范围与模型选择

预测范围

预测范围是指根据历史时间序列数据预测未来数据点的时间段。例如，根据10年记录的每日气温数据，预测下一周的气温。在这种情况下，预测范围是一周的时间。

模型选择

选择合适的预测模型是时间序列预测的关键步骤。在这个过程中，需要考虑数据的特性、模型的复杂性以及预测的准确性。通常，使用某些统计指标如AIC和BIC来帮助模型选择，这些指标帮助评估模型的拟合优良性并避免过度拟合。

时间序列预测的挑战

时间序列预测面临的主要挑战包括数据的平稳性、异常值的处理以及多变的外部环境对数据的影响。

平稳性

平稳时间序列是指其统计属性（如均值和方差）不随时间变化。对于非平稳时间序列，常用的方法包括差分和对数变换来使数据平稳。

异常值处理

异常值可能会对预测模型的准确性造成显著影响，因此在建模之前，需要对数据进行清洗和处理，以便去除或调整异常值。

时间序列的应用场景

时间序列分析在许多领域都有广泛的应用，包括但不限于：

金融市场中的股票价格预测
气候变化研究
交通流量分析
医疗健康数据监测

通过时间序列分析，企业和研究人员可以更好地理解历史数据，从而做出更加明智的决策。

时间序列中的平滑方法

平滑方法是一类用于减少时间序列数据中的随机噪声的技术，从而更好地观察数据的趋势和季节性成分。

移动平均法

移动平均法通过计算数据点的滑动平均来平滑数据。这种方法可以有效减少数据中的短期波动。

指数平滑法

指数平滑法赋予较新的数据点更高的权重，因此在处理含有趋势和季节性成分的数据时表现优异。

FAQ

问：什么是时间序列？

答：时间序列是一组按时间顺序排列的数据点，用于分析和预测随时间变化的现象。

问：时间序列分析有哪些常用模型？

答：常用模型包括AR、MA、ARMA、ARIMA、SARIMA和SARIMAX等。

问：如何处理时间序列数据中的异常值？

答：可以通过数据清洗、平滑技术和异常检测算法来处理异常值，确保预测模型的准确性。

问：时间序列分析的应用场景有哪些？

答：时间序列分析广泛应用于金融、气候研究、交通分析和医疗健康等领域。

问：如何选择合适的时间序列预测模型？

答：模型选择应基于数据特性、预测准确性和模型复杂性，同时可以使用AIC和BIC指标进行评估。

通过掌握时间序列分析的基本原理和技术，研究人员和工程师可以更好地理解和预测各种动态系统的行为，为决策提供有力的支持。