行列式的意义：几何与代数的深度解读

行列式在数学中扮演着至关重要的角色，不仅是线性代数的核心概念之一，更是在工程和科学计算中广泛应用的工具。本文将详细探讨行列式的几何意义、性质及其在实际应用中的重要性。

行列式的基本定义

行列式是一个通过特定计算方法从方阵生成的数值。它可以是实数、复数或者多项式，取决于行列式中是否包含未知数。行列式不仅仅是一个数值表，它通过特定的计算方式进一步处理这些数值，最终得到一个具有特殊意义的结果。

行列式的计算

行列式的计算方法因阶数不同而异。以下是几种常见的行列式示例：

• 一阶行列式：

  

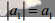
• 二阶行列式：

  

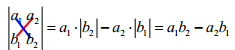
• 三阶行列式：

  

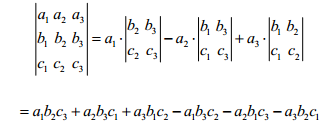
• N阶行列式：

  

这些方阵的行列式通过一系列的计算步骤得出，且每一阶数的行列式计算方法都遵循其独特的规则。

行列式的几何意义

行列式的几何意义可以从两种角度理解：

1. 静态的体积概念：行列式等于由行或列向量构成的超平行多面体的有向面积或有向体积。

2. 动态的变换比例概念：矩阵的行列式代表线性变换下图形的面积或体积的伸缩因子。

二阶行列式的几何意义

二阶行列式的几何意义体现在它在二维平面上形成的有向面积。具体而言，一个二阶行列式可以看作是平行四边形的有向面积，其邻边由行向量构成。

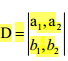
这个几何意义的另一个解释是：二阶行列式与两个向量的叉积等价。叉积的结果是一个向量，其大小即为该平行四边形的面积。这一特性在物理学中用于计算力矩等物理量。

三阶行列式的几何意义

三阶行列式则代表空间中的平行六面体的有向体积。这里的每一个行向量或列向量都是六面体的一条边，行列式的值即为该六面体的体积。当六面体的两条邻边重合时，其体积为零，对应的行列式值也为零。

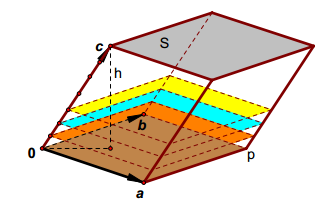
行列式的这些几何意义不仅仅是数学概念，它们在物理、工程等领域的应用中也有实际的意义。

行列式的性质

行列式的性质是其在数学中的应用基础。以下是行列式的一些重要性质：

1. 行列式的乘法性质：

   行列式的一个重要性质是对于任意两个方阵A和B，有：

   

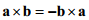
   这意味着行列式在矩阵乘法下满足交换律，即使矩阵乘法本身不满足交互律。

2. 行列式的交换性质：

   如果交换行列式的两行，行列式的值会变号。这一性质可以通过几何直观来理解：两向量在同一条直线上的平行四边形的面积为零。

3. 行列式的对角化性质：

   行列式可以通过初等行变换化为对角形，这在计算和简化过程中非常有用。

行列式的转置性质

行列式的转置性质指出：矩阵A的行列式等于其转置矩阵的行列式。这个性质在对称矩阵的研究中尤为重要，因为对称矩阵的行列式具有相同的几何意义。

行列式在实际中的应用

行列式不仅在数学中具有理论价值，还在实际应用中发挥着重要作用。以下是几个行列式的实际应用场景：

线性方程组的解法

克莱姆法则是用行列式求解线性方程组的经典方法。通过计算系数矩阵和常数项的行列式，可以得到方程组的解。

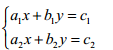
物理学中的应用

行列式在物理学中用于描述线性变换的特性。例如，在量子力学中，行列式可用于计算波函数的叠加。

行列式的进一步研究

行列式作为线性代数的基础，在数学研究中有着丰富的课题。例如，研究行列式与特征值、特征向量之间的关系，可以深入理解矩阵的性质。

FAQ

1. 问：行列式与矩阵有什么区别？

   • 答：行列式是一个数值，而矩阵是一个数表。行列式通过矩阵的元素计算得到，代表几何意义上的面积或体积。

2. 问：行列式如何用于求解线性方程组？

   • 答：通过克莱姆法则，行列式可以用于求解线性方程组。该方法通过计算系数矩阵和常数项的行列式来得到方程组的解。

3. 问：行列式在物理中有哪些应用？

   • 答：行列式在物理学中用于描述线性变换的特性，计算力矩、量子力学中的波函数叠加等。

行列式的意义不仅体现在数学理论中，更在实际应用中为我们提供了强大的工具和方法。通过对其几何意义和性质的深入理解，我们可以更好地应用行列式解决实际问题。