RSA算法详解：探索非对称加密的奥秘

什么是RSA算法

RSA算法是一种广泛应用的非对称加密算法，由罗纳德·李维斯特（Ron Rivest）、阿迪·萨莫尔（Adi Shamir）和伦纳德·阿德曼（Leonard Adleman）于1977年提出。该算法的安全性基于大数因数分解的困难性。因此，只要密钥长度足够长，RSA加密的信息在理论上是无法破解的。RSA算法的核心思想是利用两个大质数的乘积生成密钥对，其中公钥用于加密，私钥用于解密。

RSA算法示意图

RSA的魅力在于其非对称性，这意味着加密和解密使用的是不同的密钥。公钥可以公开，而私钥必须保密。RSA算法在信息加密、安全通信和数字签名等领域有着广泛的应用。

RSA加密过程详解

RSA加密过程是一个数学运算，将明文通过公钥转化为密文。该过程可以用一个通式来表示：

密文 = 明文^E mod N

在这个公式中，E和N构成了公钥。要进行RSA加密，必须先生成一对密钥对。生成公钥和私钥的步骤如下：

选择两个大质数p和q，计算N = p * q。
计算欧拉函数r = (p-1)*(q-1)。
选择一个小于r且与r互质的整数E。
计算E关于r的模反元素，命名为D，使得E * D ≡ 1 (mod r)。
公钥为(E, N)，私钥为(D, N)。

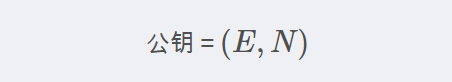
RSA加密过程

RSA解密过程

解密过程是加密过程的逆过程，使用私钥对密文进行解密。解密算法的公式为：

明文 = 密文^D mod N

其中，D为解密密钥。解密时，只有拥有私钥的人才能将密文转换回明文。这种加密和解密的互逆性使得RSA算法在信息安全领域具有极高的实用价值。

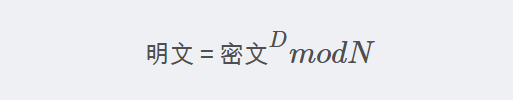
RSA解密过程

生成密钥对的详细步骤

生成RSA密钥对的过程涉及复杂的数学计算，下面是一个详细的步骤描述：

生成质数p和q

选择两个大质数p和q是生成RSA密钥对的第一步。这两个数的选择直接影响密钥的安全性。因此，质数不能太小，否则容易被破解。通常使用概率算法来验证大整数是否为质数。

计算N和欧拉函数r

一旦选择了质数p和q，计算N = p q。接着，计算欧拉函数r = (p-1) (q-1)，这一步是为了后续生成公钥和私钥做准备。

选择公钥指数E

E必须满足两个条件：1 < E < r，并且E与r互质。一般选择65537作为E，因为它是一个常用的公钥指数，能在保证安全的同时提高计算效率。

计算私钥指数D

私钥指数D是通过求解以下模反元素方程得到的：

E * D ≡ 1 (mod r)

D的计算可以通过扩展欧几里得算法来实现。

销毁质数p和q

完成密钥对的生成后，必须安全销毁质数p和q，以防止私钥被推导出来。

实践中的RSA加解密示例

为了更好地理解RSA加密算法，我们可以通过一个简单的例子来演示：

假设选择质数p = 17和q = 19，则：

计算N = 17 * 19 = 323。
计算r = (17-1)*(19-1) = 288。
选择E = 5，因为5与288互质。
计算D，使得5 * D ≡ 1 (mod 288)。通过计算可得D = 173。

公钥为(5, 323)，私钥为(173, 323)。

加密过程

假设明文是123，使用公钥加密：

密文 = 123^5 mod 323 = 240

解密过程

使用私钥解密密文：

明文 = 240^173 mod 323 = 123

Java中RSA加解密的注意事项

在Java中实现RSA加解密时，有一些重要的注意事项需要考虑：

质数的选择

选择合适的质数对RSA算法的安全性至关重要。应使用可靠的算法生成大质数，并确保随机数生成器的安全性。

密钥长度的影响

密钥长度直接影响加密强度和计算效率。虽然较长的密钥更安全，但也会降低加解密速度。通常，1024位或2048位是比较常见的选择。

加密数据长度限制

RSA加密的数据长度不能超过密钥长度减去11字节。因此，较长的数据需要使用分块加密或结合对称加密算法。

Java中实现示例

以下是Java中实现RSA加解密的简单示例：

import java.security.*;
import javax.crypto.Cipher;

public class RSADemo {
    public static void main(String[] args) throws Exception {
        KeyPairGenerator keyGen = KeyPairGenerator.getInstance("RSA");
        keyGen.initialize(2048);
        KeyPair pair = keyGen.generateKeyPair();
        PublicKey publicKey = pair.getPublic();
        PrivateKey privateKey = pair.getPrivate();

        Cipher cipher = Cipher.getInstance("RSA");

        // Encrypt
        cipher.init(Cipher.ENCRYPT_MODE, publicKey);
        byte[] encryptedData = cipher.doFinal("Hello, RSA!".getBytes());

        // Decrypt
        cipher.init(Cipher.DECRYPT_MODE, privateKey);
        byte[] decryptedData = cipher.doFinal(encryptedData);

        System.out.println("Decrypted: " + new String(decryptedData));
    }
}