递归计算时间复杂度公式深入解析

本文全面解析递归计算时间复杂度公式，包括Master公式的定义、使用方法以及不同情况下的复杂度推导。通过对递归算法的理论基础与实际应用进行详细分析，帮助读者理解如何通过公式推导递归算法的时间复杂度。这是一本有关算法设计与分析的重要指南，适合对递归算法感兴趣的学习者和从业者。

算法设计与分析概述

什么是算法设计

算法设计是计算机科学的核心，它为问题提供解决方案。算法是指令的序列，通过执行这些指令，我们可以从输入得到问题的答案。算法的设计往往需要考虑多种因素，包括时间复杂度和空间复杂度。

递归与非递归算法

根据算法是否包含递归调用，算法可以分为递归算法和非递归算法。递归算法通过将大问题分解为小问题来解决，而非递归算法则更直接地处理问题。

时间复杂度分析的重要性

在算法设计中，分析时间复杂度是至关重要的。时间复杂度帮助我们估计算法的效率，特别是在处理大规模数据时。使用渐近符号如Θ、O、Ω等，可以描述算法的执行时间与输入规模之间的关系。

非递归算法时间复杂度分析

固定时间的算法

非递归算法有时候可以在固定时间内完成任务，这种情况下的时间复杂度为O(1)。例如，一个简单的数组赋值操作不随规模n的变化而变化。

循环结构的分析

当算法包含循环结构时，时间复杂度通常由最深的循环决定。以下代码块展示了一个三重嵌套循环的例子，其时间复杂度为O(n³)。

void fun(int n){
    int x=0;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=i;j++){
            for(int k=1;k<=j;k++){
                x++; // 基本语句
            }
        }
    }
}

求和与放缩技巧

在分析非递归算法时，求和与放缩技巧常被用来简化复杂度计算，包括等差数列求和、等比数列求和等。这些技巧也在递归算法分析中广泛应用。

递归时间复杂度的数列知识应用

累加法

累加法用于递推关系式为a_{n+1} - a_n = f(n)的情况。通过累加，可以将递归问题转化为数列求和的问题。

累乘法

累乘法用于递推关系式为a_{n+1}/a_n = f(n)的情况。通过累乘，可以得到递推关系式的迭代解。

构造法

构造法通过将递推关系转化为等差或等比数列来求解。这种方法通常使用待定系数法来解决复杂递推关系。

递归时间复杂度的代入法分析

猜测解的形式

代入法的第一步是猜测递推式的解形式。这需要一定的经验和直觉，通常可以通过观察递推关系得出解的渐近形式。

数学归纳法验证

一旦猜测出解的形式，下一步是通过数学归纳法验证这个解。这涉及到证明递推关系在所有情况下都成立。

技巧与挑战

代入法具有一定的挑战性，因为猜测和验证的过程可能需要多次尝试和修改。但这种方法提供了一种强有力的工具来分析递归时间复杂度。

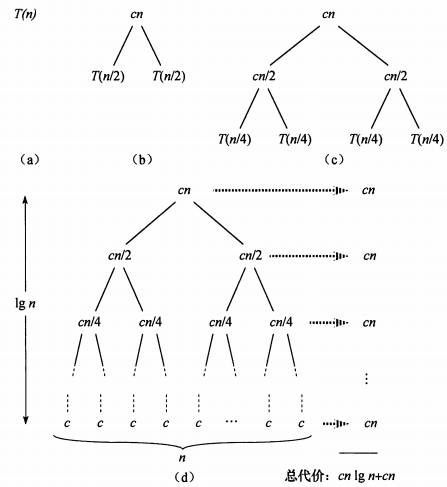
递归树模型解析递归时间复杂度

递归树的构建

递归树是分析递归算法时间复杂度的一种直观方法。通过将递归过程抽象为树结构，可以清晰地看到每一层的计算代价。

层级代价求和

在递归树中，每一层的代价需要求和，最终得到整个递归过程的总代价。例如，对于T(n) = 2T(n/2) + O(n)，递归树的总代价为Θ(n log n)。

优势与应用

递归树模型的优势在于其直观性，特别是在分析复杂递推关系时，它能提供一种清晰的可视化工具。

递归树模型

主方法的递归时间复杂度推导

主方法介绍

主方法提供了一种系统化的方法来解决特定形式的递归方程。其一般形式为T(n) = aT(n/b) + f(n)。

主定理的应用

主定理通过对f(n)与n^{log_b a}的比较，提供了三种可能的时间复杂度解：O(n^{log_b a})，O(n^d log n)，O(f(n))。

实际应用案例

主方法在许多经典算法中被应用，如归并排序和快速排序。理解主方法有助于我们分析和设计高效的递归算法。

Master公式及其推导过程

Master公式的定义

Master公式是一种分析递归时间复杂度的工具，适用于分治策略算法。其形式为T(n) = aT(n/b) + O(n^d)。

变量的意义

在公式中，a代表每次递归调用的子问题数量，b表示子问题规模缩小的比例，d则是递归外代码的时间复杂度参数。

通过Master公式推导时间复杂度

Master公式为不同情况提供了明确的时间复杂度推导规则，使得分析递归算法的复杂度变得简单和直观。

Master公式练习题

FAQ

问：什么是算法设计，为什么它在计算机科学中如此重要？

答：算法设计是计算机科学的核心，涉及为各种问题提供解决方案。算法是指令的序列，通过这些指令，我们能从输入得到答案。算法设计考虑多种因素，包括时间复杂度和空间复杂度，决定了算法在大规模数据处理时的效率。

问：递归与非递归算法有何区别？

答：递归算法和非递归算法的区别在于是否包含递归调用。递归算法通过将大问题分解为小问题来解决，而非递归算法则更直接地处理问题。

问：为什么分析时间复杂度对算法设计至关重要？

答：时间复杂度分析有助于估计算法的效率，特别是在处理大规模数据时。通过渐近符号如Θ、O、Ω等，可以描述算法的执行时间与输入规模之间的关系，从而帮助设计高效的算法。

问：如何使用递归树模型分析递归算法的时间复杂度？

答：递归树模型通过将递归过程抽象为树结构，直观地展示每一层的计算代价。通过层级代价求和，可以得到整个递归过程的总代价。例如，对于T(n) = 2T(n/2) + O(n)，递归树的总代价为Θ(n log n)。

问：什么是Master公式？如何用于推导递归时间复杂度？

答：Master公式是一种分析递归时间复杂度的工具，适用于分治策略算法，形式为T(n) = aT(n/b) + O(n^d)。通过比较f(n)与n^{log_b a}，Master公式提供了三种可能的时间复杂度解：O(n^{log_b a})，O(n^d log n)，O(f(n))，使得分析递归算法的复杂度变得简单和直观。