ARIMA中参数选择及相关问题

ARIMA模型概述

ARIMA模型，即自回归积分滑动平均模型，是一种常用的时间序列分析工具。其核心思想是通过对非平稳时间序列进行差分操作，使其转化为平稳序列，然后利用自回归（AR）和移动平均（MA）方法进行建模。ARIMA模型的参数主要包括自回归项数(p)、差分次数(d)和移动平均项数(q)。对于时间序列分析，合理选择ARIMA模型的参数是非常关键的，它直接影响模型的预测精度。

参数选择的基本原则

在进行ARIMA模型参数选择时，通常有两种方法：一种是利用自相关函数(ACF)和偏自相关函数(PACF)图的截尾和拖尾特性，另一种是通过信息准则如AIC和BIC来选择最优参数。ACF和PACF图用于识别序列的自相关性和偏自相关性，从而帮助确定p和q的值。而AIC和BIC等信息准则则提供了一种更为定量的模型选择方法。

ACF和PACF图的应用

自相关函数(ACF)和偏自相关函数(PACF)图是ARIMA模型参数选择的重要工具。通过观察ACF和PACF图，可以判断序列是否需要差分，以及p和q的可能取值范围。一般来说，ACF图用于判断q值，而PACF图用于判断p值。

信息准则的应用

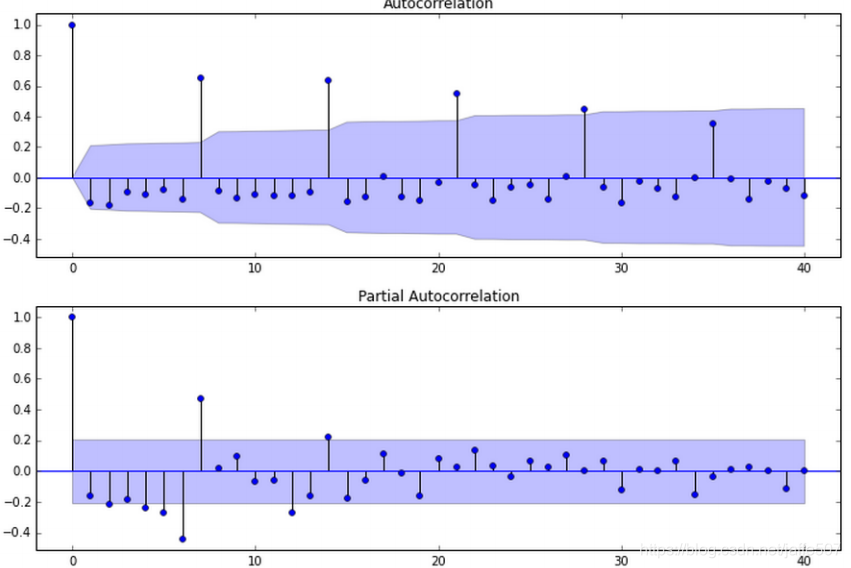
AIC和BIC信息准则是选择ARIMA模型参数的另一种常用方法。AIC和BIC通过对模型复杂度和拟合优度进行平衡，帮助选择最优的p、d、q组合。一般来说，AIC和BIC值越小，模型越优。

差分操作与序列平稳性

差分操作是将非平稳时间序列转化为平稳序列的常用方法。对于一个非平稳序列，通过一定次数的差分操作，可以消除其趋势成分，使其成为平稳序列。差分次数d的选择通常通过观察序列的趋势特性和单位根检验来确定。

ARIMA模型的建立与验证

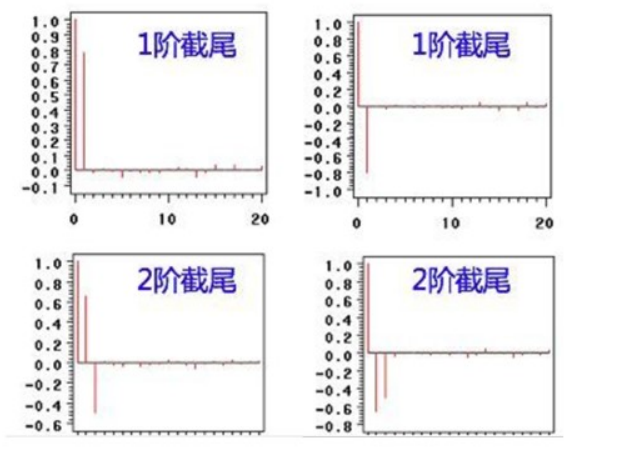
在确定了ARIMA模型的参数后，接下来就是模型的建立和验证。模型的建立通常使用历史数据进行训练，而验证则需要通过检验模型的残差序列来判断模型的适用性。残差的ACF和PACF图可以帮助判断模型是否充分拟合数据。

模型的诊断与调整

在模型验证阶段，如果残差序列存在显著的自相关性，则说明模型可能存在问题，需要调整参数或增加模型复杂度。例如，可以考虑增加AR或MA项，或者重新进行差分操作。

实际应用中的注意事项

在实际应用中，ARIMA模型的建立不仅仅是参数选择的问题，还需要考虑数据的质量、季节性因素以及外部变量的影响。这些因素都会影响模型的预测效果，需要在建模过程中加以考虑。

FAQ

问：ARIMA模型适用于所有时间序列吗？

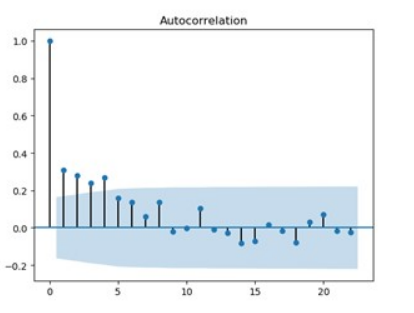
答：ARIMA模型适用于平稳时间序列或通过差分可以转化为平稳的序列。然而，对于具有季节性或其他复杂特性的序列，可能需要使用SARIMA等扩展模型。

问：如何确定差分次数d？

答：差分次数d的确定通常通过观察序列的趋势特性和单位根检验来确定。可以尝试进行一阶或二阶差分，直到序列达到平稳为止。

问：为什么我的模型预测效果不好？

答：模型预测效果不好可能是由于参数选择不当、模型未充分拟合、数据质量问题或忽略了外部变量的影响。需要对模型进行诊断和调整，以提高其预测效果。

问：ARIMA模型能否用于实时预测？

答：ARIMA模型可以用于实时预测，但需要确保数据的实时性和模型参数的及时更新。同时，模型需要在真实环境中进行充分的测试和验证。

问：如何在Python中实现ARIMA模型？

答：可以使用statsmodels库中的ARIMA类来实现ARIMA模型。通过fit方法进行模型训练，predict方法进行预测。

from statsmodels.tsa.arima.model import ARIMA

model = ARIMA(data, order=(p, d, q))
model_fit = model.fit()
forecast = model_fit.predict(start=start_date, end=end_date, dynamic=True)

通过以上内容，我们详细探讨了ARIMA模型的参数选择问题及其在实际应用中的注意事项。合理选择ARIMA模型的参数，可以显著提高时间序列预测的精度。