Minimax 源码分析与实现：探索算法核心与应用

Minimax算法的基本原理

Minimax算法，也被称为极小化极大算法，是计算机科学中一种重要的博弈算法。它广泛应用于两方对弈的游戏中，例如国际象棋、五子棋等。算法的基本思想是通过构建决策树评估每个可能的游戏状态，并在最坏的情况下选择最佳策略。Minimax假设对手会尽可能完美地进行决策，因此每一步都要考虑对方可能的最佳反应。

在这类游戏中，玩家通常需要在自己的回合中选择一个能够最大化自身利益的操作，而对手则会选择一个最小化我方利益的操作。这种策略使得每次选择都在最大化和最小化之间进行权衡，从而为玩家找到最佳的行动方案。

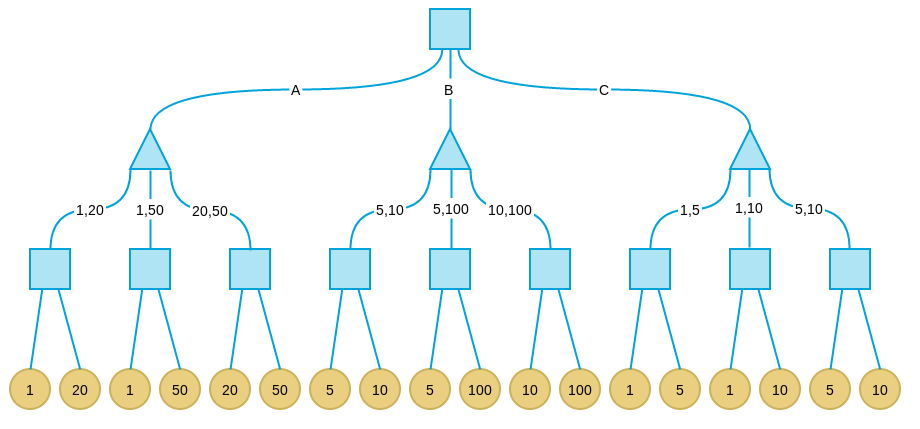
Minimax 算法示意图

Minimax算法的实现步骤

构建游戏状态树

首先，Minimax算法需要构建一个游戏状态树，其中每个节点代表一种可能的游戏状态。树的根节点代表当前的初始状态，而子节点代表可能的后续状态。通过递归遍历这棵树，算法可以计算出每个状态的价值。

评估函数的设计

评估函数是Minimax算法的核心组件之一。它用于评估每个叶节点的价值，通常通过对游戏中的特定因素进行加权来实现。例如，在国际象棋中，评估函数可能考虑棋子位置、棋子总数等因素，以此来评估当前局面的优劣。

function evaluateBoard(board) {
    let score = 0;
    // 评估每个棋子的价值
    board.forEach(row => {
        row.forEach(piece => {
            score += getPieceValue(piece);
        });
    });
    return score;
}

递归搜索与剪枝优化

在构建完评估函数后，Minimax通过递归搜索所有可能的游戏状态，从而选择最佳路径。然而，由于状态空间可能非常庞大，直接搜索所有状态并不实际。此时，Alpha-beta剪枝算法可以帮助优化搜索过程，去除不必要的分支，从而提高效率。

实战案例：井字棋中的应用

井字棋是一个经典的二人游戏，适合作为Minimax算法的示例。通过Minimax，程序可以在每一步都选择最优的下子位置，确保不会输。

游戏状态表示

在井字棋中，棋盘可以用一个3×3的数组表示，其中每个元素表示一个位置的状态（空、X或O）。玩家的目标是通过选择合适的位置，率先在行、列或对角线上连成三个相同的标记。

实现Minimax算法

function minimax(board, depth, isMaximizing) {
    let scores = {X: 10, O: -10, tie: 0};
    let result = checkWinner(board);
    if (result !== null) {
        return scores[result];
    }

    if (isMaximizing) {
        let bestScore = -Infinity;
        for (let i = 0; i < board.length; i++) {
            for (let j = 0; j < board[i].length; j++) {
                if (board[i][j] === '') {
                    board[i][j] = 'X';
                    let score = minimax(board, depth + 1, false);
                    board[i][j] = '';
                    bestScore = Math.max(score, bestScore);
                }
            }
        }
        return bestScore;
    } else {
        let bestScore = Infinity;
        for (let i = 0; i < board.length; i++) {
            for (let j = 0; j < board[i].length; j++) {
                if (board[i][j] === '') {
                    board[i][j] = 'O';
                    let score = minimax(board, depth + 1, true);
                    board[i][j] = '';
                    bestScore = Math.min(score, bestScore);
                }
            }
        }
        return bestScore;
    }
}

Alpha-beta剪枝算法简介

Alpha-beta剪枝是Minimax算法的优化版本，通过剪枝技术减少需要评估的节点数量。它通过维护两个变量alpha和beta来记录当前玩家的最佳选择和对手的最差反应，从而有效地剪去不必要的分支。

Alpha-beta剪枝示意图

Alpha-beta剪枝的实现

function alphabeta(node, depth, alpha, beta, maximizingPlayer) {
    if (depth === 0 || isTerminal(node)) {
        return evaluate(node);
    }
    if (maximizingPlayer) {
        let value = -Infinity;
        for (const child of node.children) {
            value = Math.max(value, alphabeta(child, depth - 1, alpha, beta, false));
            alpha = Math.max(alpha, value);
            if (alpha >= beta) {
                break; // Beta剪枝
            }
        }
        return value;
    } else {
        let value = Infinity;
        for (const child of node.children) {
            value = Math.min(value, alphabeta(child, depth - 1, alpha, beta, true));
            beta = Math.min(beta, value);
            if (beta <= alpha) {
                break; // Alpha剪枝
            }
        }
        return value;
    }
}