一维数据转二维图像的方法

背景介绍

在现代数据分析和机器学习的背景下，将一维时间序列数据转换为二维图像是一种常用的方法。这样的转换不仅可以帮助我们更好地理解数据的模式和趋势，还能够通过图像处理技术进一步分析数据。深度学习技术在图像识别领域的突破，使得研究者们开始探索如何将一维数据转换为更易于处理的二维图像形式。

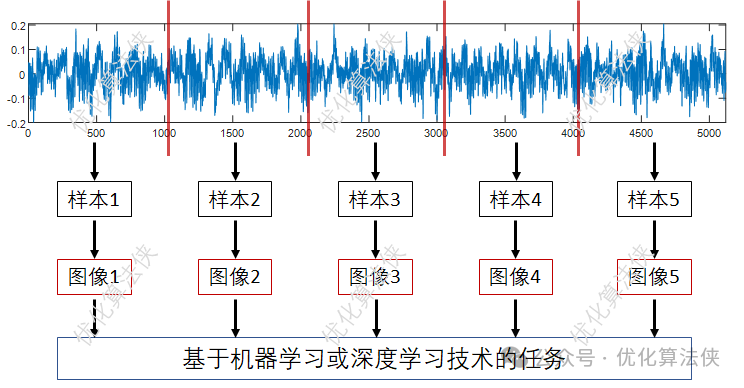
时频类方法主要通过分析信号的频率分布来将一维数据转换为二维图像。这些方法包括梅尔频谱图、短时傅里叶变换、S变换等。每种方法都有其独特的优势，适用于不同的应用场景。

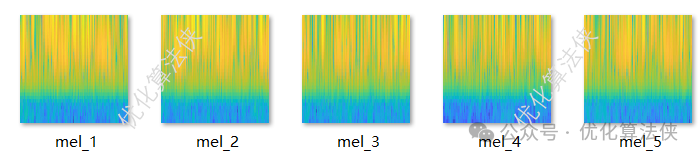
梅尔频谱图是一种常用的音频信号处理工具，能够通过频率和时间两个维度来展示信号的变化。其主要优势在于能够保留信号的时频特征，适用于语音识别和音乐分析。

梅尔频谱图

短时傅里叶变换通过窗函数将信号分为多个片段，对每个片段进行傅里叶变换以获得时频谱。这种方法在音频信号分析中应用广泛，能够有效处理非平稳信号。

import scipy.signal as scisig

fs = 10e3  # 采样频率
x = ...  # 输入信号
t, f, Zxx = scisig.stft(x, fs)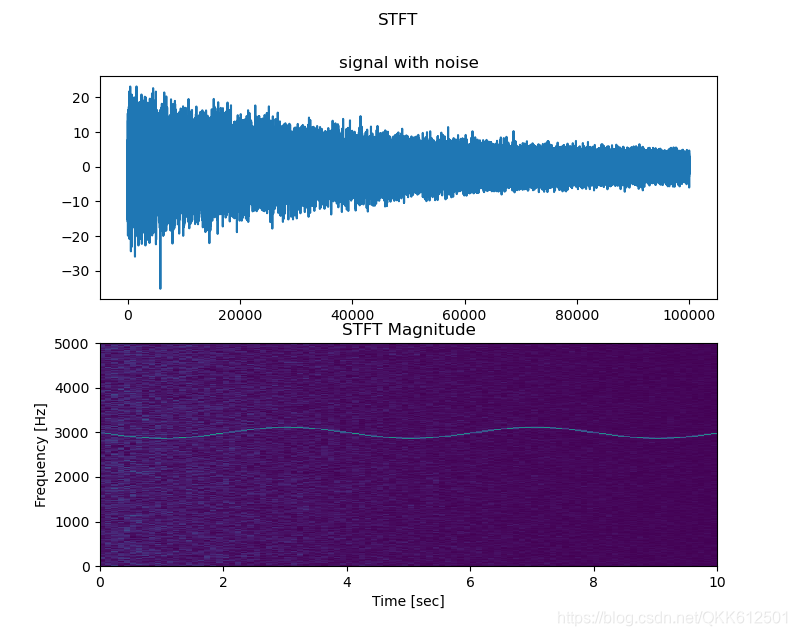

STFT示例

时域转换类方法通过直接对时间序列进行几何变换，将一维数据映射为二维图像。这类方法包括格拉姆角和场、递归图等。

格拉姆角和场通过将缩放后的序列数据从直角坐标系转换到极坐标系，提取时间相关性。该方法在金融数据分析中被广泛应用。

GASF示例

递归图是用来分析时间序列的周期性和混沌特征的重要工具。它通过展示数据点之间的相似性来揭示序列的内在结构。

from pyts.image import RecurrencePlot

rp = RecurrencePlot()
X_new = rp.transform(X)

递归图示例

在数据分析过程中，选择合适的方法进行一维到二维转换非常重要。不同方法适合于不同类型的数据和分析需求。例如，音频信号更适合使用时频类方法，而金融数据则可能更适合时域转换类方法。

问：为什么要将一维数据转换为二维图像？
- 答：转换为二维图像可以利用图像处理技术，更直观地分析数据的模式和趋势，特别是在使用深度学习进行分类和识别时效果显著。
问：如何选择合适的一维数据转二维图像的方法？
- 答：选择方法应该根据数据特性和分析目标来定。例如，音频信号分析常用时频类方法，而金融数据分析常用时域转换类方法。
问：这些方法可以应用于实时数据处理吗？
- 答：可以。许多方法支持实时数据处理，特别是短时傅里叶变换，可以实时分析音频信号的频谱变化。