平均曲率与几何曲面的魅力

平均曲率作为描述几何体弯曲特性的关键指标，广泛应用于数学、物理和工程领域。通过理解平均曲率，我们可以更好地分析和设计复杂的几何结构。在建筑设计中，利用平均曲率可以创造出更具美感的结构；在机械工程中，它有助于提高零件的性能和耐久性。此外，通过曲率分析，我们可以探讨曲面的内蕴特性，了解其在空间中的位置和形状。

曲率基本概念

外在曲率与内蕴曲率

曲率是几何中用来描述形状弯曲程度的一个基本概念。它可以分为外在曲率和内蕴曲率。外在曲率是通过将几何体嵌入到欧氏空间中来定义的，通常用于分析曲面或曲线的外部形态。而内蕴曲率则是直接在黎曼流形上定义的，反映了几何体自身的属性。

曲率的基本公式

在数学上，曲率可以通过各种公式来定义。例如，对于一个简单的圆，其曲率可以用半径的倒数来表示。半径越小，曲率越大。这种基本的定义为复杂曲线的曲率计算提供了基础。

曲率的应用领域

曲率广泛应用于几何学、物理学和计算机科学等多个领域。在工程应用中，曲率可以帮助了解材料性能，在计算机图形学中则用于生成逼真图像。

函数图像曲率计算

平面曲线曲率公式

在解析几何中，函数图像的曲率可以通过导数来计算。对于给定的函数 $y = f(x)$，其曲率可以表示为：

kappa = frac{|f^{primeprime}(x)|}{(1+f^{prime2}(x))^{3/2}}

极坐标方程的曲率

对于极坐标方程给出的曲线 $r = r(theta)$，其曲率可以表示为：

kappa(theta) = frac{|r^2 + 2r^{prime2} – rr^{primeprime}|}{(r^2 + r^{prime2})^{3/2}}

曲率计算的实际意义

这些公式提供了对曲线在特定点上如何弯曲的数学描述，帮助我们在各个领域进行更深入的分析和应用。

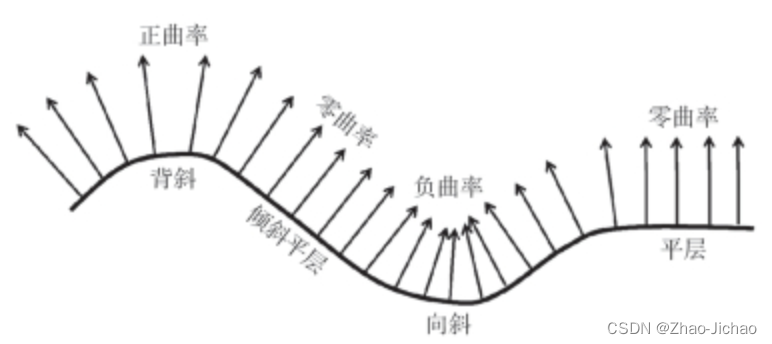
曲率范例解析

抛物线曲率计算

考虑一个抛物线 $y = frac{x^2}{2p}$，通过代入曲率公式，我们可以计算出其在不同点的曲率。首先，计算一阶导数和二阶导数：

f^{prime}(x) = frac{x}{p}, quad f^{prime2}(x) = frac{x^2}{p^2}, quad f^{primeprime}(x) = frac{1}{p}

然后，将这些值代入曲率公式：

kappa = frac{|1/p|}{(1 + x^2/p^2)^{3/2}}

结果分析

这种计算过程展示了如何通过数学公式精确地描述曲线的弯曲特性，为各种实际应用提供了理论基础。

其他函数曲率

除了抛物线，我们也可以对椭圆和双曲线等其他函数进行类似的曲率计算，方法类似，都需要用到导数。

三维空间曲面曲率

高斯曲率

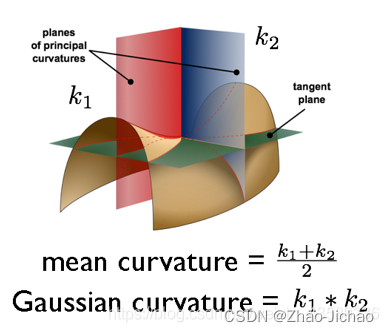
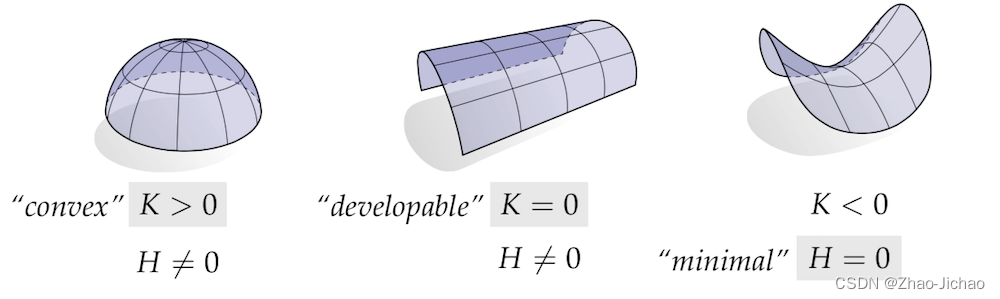
高斯曲率是主曲率的乘积，用于描述曲面的内蕴特性。它可以帮助我们判断曲面在某个点是局部凸（高斯曲率为正）还是局部鞍形（高斯曲率为负）。

G = kappa_1 kappa_2

平均曲率概念

平均曲率是主曲率的算术平均值，表示曲面在某一点的整体弯曲特性。平均曲率在计算曲面上的物理特性时非常重要，例如在材料科学和流体力学中。

H = frac{kappa_1 + kappa_2}{2}

三维曲面应用

在三维空间中，曲面曲率的分析有助于理解复杂结构的形态和性质，例如在建筑设计和生物学中。

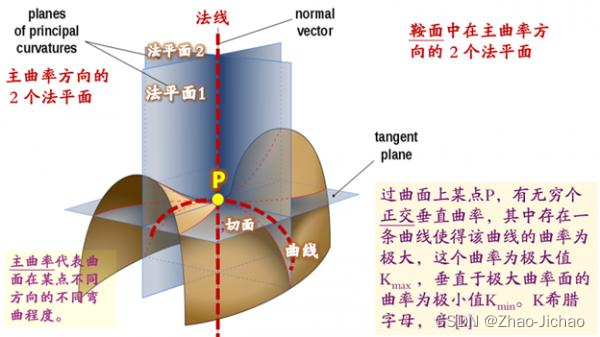
法曲率与方向性

法曲率定义

法曲率指的是曲面在某一点沿着不同方向的弯曲程度。它通过在该点的法向量和切向量确定的平面与曲面的交线的曲率来定义。

法曲率的计算

在计算法曲率时，需选择合适的法向量和切向量，这样才能得到精确的法曲率值。

法曲率的应用

法曲率在材料工程中用于评估材料的抗弯性能，在地质学中用于分析地壳形变。

高斯曲率与内蕴特性

高斯曲率计算

高斯曲率通过主曲率的乘积来表示，反映了曲面的内蕴特性，不依赖于外部空间的嵌入。

G = kappa_1 kappa_2

内蕴特性的重要性

内蕴特性揭示了曲面自身的性质，对于理解几何形状在不同环境中的表现至关重要。

应用实例

高斯曲率在图像处理和计算机视觉中用于识别和分类三维物体。

曲率实际应用

建筑与设计

在建筑设计中，了解曲面的曲率可以帮助设计师创造出更具美感和功能性的结构。例如，现代建筑中常见的流线型设计。

工程与机械

在机械工程中，精确计算曲率可以提高零件的耐久性和性能。曲率分析有助于优化机械零件的设计，使其更加坚固和耐用。

计算机科学

在计算机图形学中，曲率用于生成逼真的三维模型和图像，帮助实现更为真实的视觉效果。

FAQ

问：什么是曲率，如何区分外在曲率和内蕴曲率？

• 答：曲率是几何中用来描述形状弯曲程度的基本概念。外在曲率是通过将几何体嵌入到欧氏空间中来定义的，适用于分析曲面或曲线的外部形态。内蕴曲率直接在黎曼流形上定义，反映了几何体自身的属性。

问：如何计算平面曲线的曲率？

• 答：对于一个给定函数 $y = f(x)$，其曲率可以通过导数来计算，公式为：

  kappa = frac{|f^{primeprime}(x)|}{(1+f^{prime2}(x))^{3/2}}

  此公式帮助我们理解曲线在特定点的弯曲程度。

问：极坐标方程的曲率计算公式是什么？

• 答：对于极坐标方程给出的曲线 $r = r(theta)$，其曲率计算公式为：

  kappa(theta) = frac{|r^2 + 2r^{prime2} – rr^{primeprime}|}{(r^2 + r^{prime2})^{3/2}}

  该公式用于分析极坐标系下的曲线形态。

问：什么是高斯曲率，它与内蕴特性有何关系？

• 答：高斯曲率是主曲率的乘积，描述了曲面的内蕴特性，不依赖于外部空间的嵌入。它反映了曲面在某点的局部形态，如局部凸或鞍形。高斯曲率在图像处理和计算机视觉中用于识别和分类三维物体。

问：平均曲率在三维空间的曲面分析中有什么作用？

• 答：平均曲率是主曲率的算术平均值，表示曲面在某一点的整体弯曲特性。它在计算曲面上的物理特性时非常重要，应用于材料科学和流体力学中，帮助分析材料的性能和流动特性。