最大似然估计方法详解

极大似然原理

极大似然原理是概率论在统计学中的应用，核心思想是通过对已发生事件概率的最大化来进行参数估计。在一个随机试验中，许多事件都有可能发生，概率大的事件发生的概率也大。因此，当某一事件发生，我们有理由认为该事件的发生概率比其他事件要大。

例如，假设一个箱子里有红色和黑色两种颜色的球，数量分别为10个和1个。我们并不知道哪种颜色的球为10个，这时我们随机从箱子里拿出一个球，如果这个球是红色的，我们就认为盒子里红球有10个，黑球有1个。

极大似然估计概述

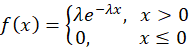
极大似然估计（Maximum Likelihood Estimation, MLE）是一种统计推断方法，旨在通过给定的数据找到使观测数据出现概率最大的参数值。极大似然估计法由高斯和费希尔先后提出，是被使用最广泛的一种参数估计方法，基于直观的极大似然原理。

极大似然估计的基本思想

极大似然估计的基本思想是利用已知的样本结果信息，反推最有可能导致这些样本结果出现的模型参数值。换句话说，极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。通过若干次试验，观察结果，利用试验结果得到某个参数值能够使样本出现的概率为最大。

似然函数与其构建

似然函数是一种关于统计模型中参数的函数，表示模型参数中的似然性，用 L 表示。给定输出 x 时，关于参数 θ 的似然函数 L(θ|x) 在数值上等于给定参数 θ 后变量 x 的概率。

似然函数的定义

似然性（likelihood）与概率（possibility）同样可以表示事件发生的可能性大小，但是二者有着很大的区别：

概率 p(x|θ) 是在已知参数 θ 的情况下，发生观测结果 x 的可能性大小。
似然性 L(θ|x) 则是从观测结果 x 出发，推断分布函数的参数 θ 的可能性大小。

最大似然估计的应用案例

例子：球的颜色估计

假设有一个罐子，里面有黑白两种颜色的球，数目多少不知。我们想知道罐中白球和黑球的比例，但不能把罐中的球全部拿出来数。我们可以通过抽样来估计罐中黑白球的比例。假如在一百次抽样中，有七十次是白球，请问罐中白球所占的比例最有可能是多少？

通过极大似然估计，我们可以假设罐中白球的比例是 p，那么黑球的比例就是 1-p。因此，我们可以通过概率计算得出白球的比例。

例子：全国人民年均收入的估计

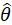
假设我们要统计全国人民的年均收入，收入服从正态分布，但该分布的均值与方差未知。我们可以选取一个城市或乡镇的人口收入，作为我们的观察样本结果。通过最大似然估计来获取正态分布的参数。

最大似然估计的优缺点

优点

高效性：在一定条件下，最大似然估计是渐近无偏的，即样本足够大时估计值逼近真值。
普适性：适用于多种类型数据和模型，灵活性强。

缺点

计算复杂：对于某些复杂模型，似然函数难以求解，计算量大。
依赖样本：估计的准确性依赖于样本量和样本质量。样本量不足时，可能产生偏差。

最大似然估计与其他估计方法比较

与最小二乘法比较

最小二乘法主要用于线性回归模型，而最大似然估计适用于更广泛的统计模型。两者在处理误差分布假设上有所不同，最小二乘法假设误差为正态分布，而最大似然估计不受此限制。

与贝叶斯估计比较

贝叶斯估计利用先验分布和观测数据进行参数估计，而最大似然估计仅依赖于观测数据。贝叶斯估计能处理参数的不确定性，但计算复杂度较高。

实际应用中的最大似然估计

最大似然估计在机器学习、经济学、生物统计学等领域有广泛应用。例如，在机器学习中用于模型参数的优化；在经济学中用于市场分析和定价模型的参数估计；在生物统计学中用于基因组数据的分析。

FAQ

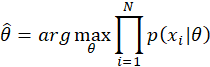
问：最大似然估计与贝叶斯估计有什么区别？
- 答：最大似然估计仅依赖于观测数据，而贝叶斯估计结合先验分布和观测数据来进行参数估计。
问：在什么情况下使用最大似然估计？
- 答：最大似然估计适用于需要估计参数的各种统计模型，尤其是在样本量较大且数据独立同分布时效果最佳。
问：最大似然估计是否总是无偏的？
- 答：不是，最大似然估计在样本量不足时可能产生偏差，但在样本量足够大时，渐近无偏。
问：最大似然估计如何处理多参数模型？
- 答：最大似然估计可以通过多维优化技术，如梯度下降法，来求解多参数模型的最优参数。
问：最大似然估计的计算复杂度如何？
- 答：计算复杂度取决于模型的复杂度和参数的数量，对于复杂模型，计算复杂度较高。