并积转置：深度学习中的关键技术

一、并积转置的背景

在深度学习中，卷积神经网络（CNN）是处理图像数据的主要工具。卷积操作通过在输入图像上滑动一个卷积核来提取特征，从而实现对图像的降维。然而，在一些应用中，如图像生成和语义分割，需要将低分辨率的特征图恢复到原始大小。为了实现这一目标，并积转置（也称为转置卷积或反卷积）成为了一个关键的技术。

图1 上采样示例

并积转置通过学习可调整的参数，能够在神经网络中自动寻找最佳的上采样方式，超越了传统插值方法（如双线性插值和双立方插值）带来的局限性。

并积转置广泛应用于需要高精度重构的场景中，例如：

普通卷积通过对输入特征图施加卷积核进行特征提取，通常实现从大尺寸到小尺寸的降采样。其操作本质上是多对一的映射，意味着多个输入特征映射到一个输出特征。

在这里插入图片描述

并积转置则反其道而行之，通过将卷积核反向应用，达到将一个输入特征扩展为多个输出特征的效果，从而实现图像的上采样。

在这里插入图片描述

为了理解并积转置的运作原理，我们可以从数学上推导其计算过程。假设有一个输入矩阵和一个卷积核，普通卷积将输入矩阵展平为一列向量，与卷积核的转换矩阵进行矩阵乘法，得出输出。

而在并积转置中，我们将其逆向操作：转换矩阵的转置与输出向量相乘，恢复成输入矩阵的形状。这种逆向计算体现了一对多的映射关系。

图2 转置后卷积矩阵运算示例

并积转置的输出大小可以通过步长、填充和卷积核大小等参数来控制。

当步长为1时，并积转置的输出大小等于输入大小加上卷积核大小减1。这相当于在输入元素之间插入零值，然后应用普通卷积。

当步长大于1时，并积转置的输出会更加复杂。为了达到期望的输出尺寸，常需要在输入矩阵中插入更多的零值，并调整填充量以匹配输出形状。

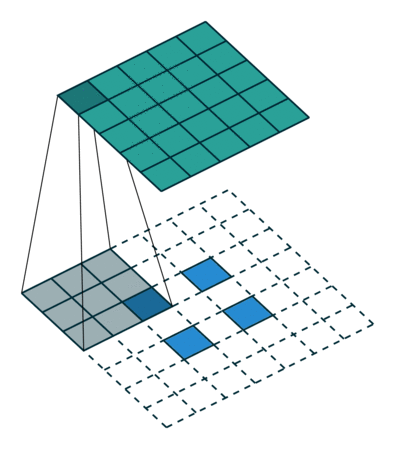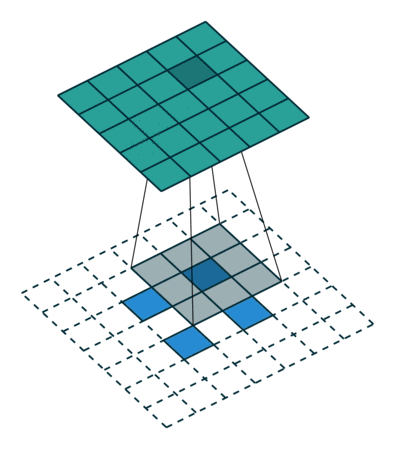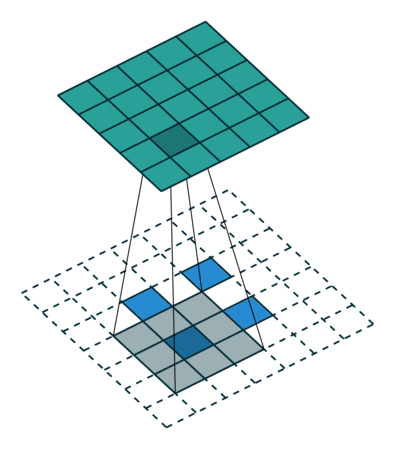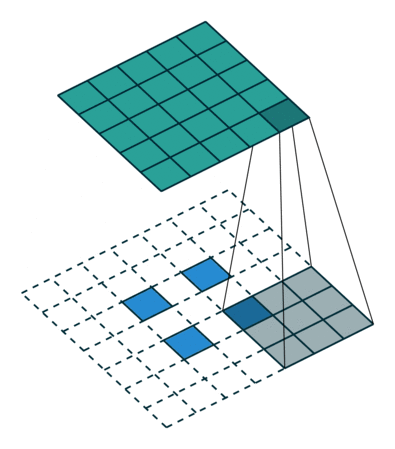图3 s=2 时，转置卷积运算示例

并积转置是深度学习中用于上采样的一种重要技术。它通过可学习的参数，提供了一种灵活的方式来恢复图像尺寸，并在图像生成和语义分割等领域得到广泛应用。然而，使用时需注意其可能带来的棋盘效应，并借助改进的方法进行优化。

问：并积转置和反卷积是同一种操作吗？
- 答：是的，并积转置和反卷积通常指的是同一种操作，但反卷积的名称可能引起误解，因其不是真正的卷积逆运算。
问：为什么并积转置会引起棋盘效应？
- 答：棋盘效应通常是由于不当的卷积核大小和步长选择，导致输出图像中出现不规则的网格图案。可以通过调整参数或使用插值方法加以缓解。
问：并积转置在GAN中如何应用？
- 答：在生成对抗网络中，生成器利用并积转置从低维噪声生成高分辨率图像，使得生成的图像更为逼真。