数学符号大全及应用解析

数学符号是数学语言的重要组成部分，它们以简洁、准确的形态表达复杂的数学概念和运算。本文将全面介绍数学符号的种类、用途以及在各个数学分支中的应用，旨在为读者提供一个全面的数学符号参考手册。

几何符号详解

几何学是研究形状、大小和空间位置的学科，其中几何符号扮演着至关重要的角色。以下是一些基本的几何符号及其含义：

垂直与平行

• ⊥ 表示垂直，用来描述两条直线或者线段在空间中彼此垂直的关系。
• ∥ 表示平行，用来描述两条直线或者线段在空间中永不相交的性质。

角度与圆

• ∠ 表示角度，用来量度两条射线之间的夹角大小。
• ⊙ 表示圆，用来描述所有与给定点（圆心）距离相等的点的集合。

三角形与全等

• △ 表示三角形，是几何中最基本的多边形。
• ≡ 表示全等，用来说明两个几何图形在形状和大小上的一致性。

代数符号详述

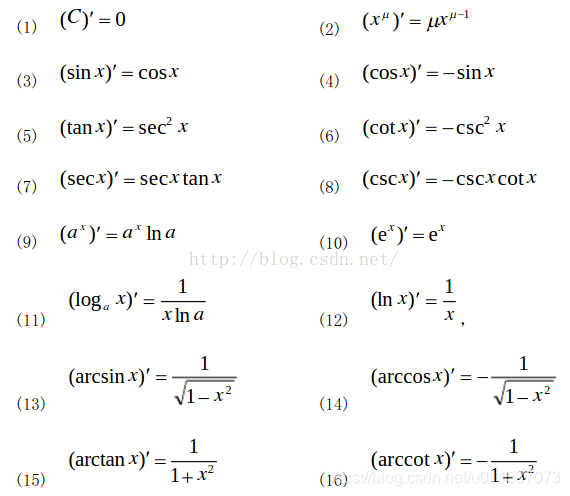
代数符号在数学中用来表示未知量、方程和不等式等概念。以下是一些关键的代数符号及其含义：

未知量与计算

• ∝ 表示成正比，用来描述两个量之间的线性关系。
• ∨ 和 ∧ 分别表示逻辑或和逻辑与，常用于描述复杂的条件语句。

不等式与无限

• ∞ 表示无穷大，用来描述趋向于无限大的趋势或者数量。
• ≈ 表示近似等于，用来表达两个数值在一定误差范围内的接近程度。

运算符号的实际应用

运算符号是进行数学计算的基础，它们定义了基本的数学操作。以下是一些基本的运算符号及其应用：

加法与减法

• + 和 – 分别表示加法和减法，是最基本的算术运算。

例：

5 + 3 = 8

10 - 4 = 6

乘法与除法

• × 和 ÷ 分别表示乘法和除法，用于计算两个数的乘积和商。

例：

8 × 2 = 16

20 ÷ 4 = 5

集合符号的重要性

集合论是数学的基础分支之一，集合符号在描述集合的关系和运算中起着核心作用。以下是一些基本的集合符号及其含义：

并集与交集

• ∪ 表示两个集合的并集，包含所有属于任一集合的元素。
• ∩ 表示两个集合的交集，包含同时属于两个集合的元素。

属于与包含

• ∈ 表示属于，用来说明某个元素是某个集合的成员。
• ⊆ 和 ⊂ 表示子集关系，用来描述集合之间的包含关系。

数学符号的逻辑推理

逻辑推理是数学证明中不可或缺的一部分，以下是一些基本的推理符号及其含义：

蕴含与等价

• ⇒ 表示蕴含，用来说明如果条件A成立，则条件B也成立。
• ⇔ 表示等价，用来说明两个命题的真假情况完全相同。

否定与合取

• ¬ 表示否定，用来表达命题的对立面。
• ∧ 表示合取，用来连接多个命题，只有当所有命题都为真时，合取命题才为真。

数学符号在微积分中的应用

微积分是研究变化率和累积量的数学分支，以下是一些微积分中常用的符号及其应用：

导数与积分

• dx 表示微分，用来描述函数在某一点的变化率。
• ∫ 表示积分，用来计算函数在某个区间的累积量。

基本初等函数求导公式

微分方程

微分方程是描述函数与其导数之间关系的方程，广泛应用于物理学和工程学中。

FAQ

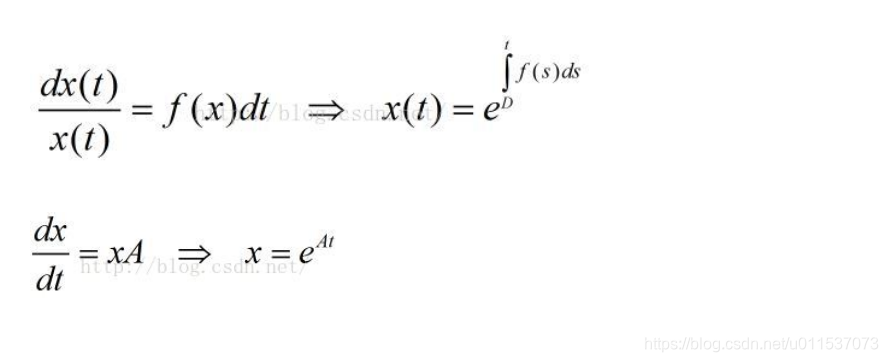
1. 问：数学符号有哪些主要类别？
   答：数学符号主要分为几何符号、代数符号、运算符号、集合符号和推理符号等类别。

2. 问：集合符号中的并集和交集有什么区别？
   答：并集包含两个集合中所有的元素，而交集只包含两个集合共有的元素。

3. 问：微积分中的导数和积分分别表示什么？
   答：导数表示函数在某一点的变化率，积分表示函数在某个区间的累积量。

4. 问：如何理解逻辑推理中的蕴含和等价？
   答：蕴含表示如果一个命题为真，则另一个命题也必须为真；等价表示两个命题在逻辑上是等价的，即它们具有相同的真值。

5. 问：微分方程在实际问题中有哪些应用？
   答：微分方程在物理学、工程学等领域中有着广泛的应用，如描述物体的运动、信号的传播等。