冪處的数学概念与应用

冪處的数学概念与应用

在数学分析中，冪處（或幂级数）是一个重要的概念，它不仅涉及到数学的基本运算，还在许多科学领域中扮演着关键角色。本文将深入探讨冪處的定义、性质、应用以及相关的数学公式。

1. 冪處的定义

冪處是指在一个给定区间内，以无穷级数的形式表示的函数，其中每一项都是一个幂函数乘以常数。其一般形式为：

[ sum_{n=0}^{infty} a_nx^n = a_0 + a_1x + a_2x^2 + cdots + a_nx^n + cdots ]

其中，(a_0, a_1, a_2, ldots, a_n, ldots)称为幂级数的系数。冪處可以用来表示许多常见的函数，也可以用于逼近复杂函数。

2. 冪處的性质

冪處具有以下几个重要性质：

2.1 连续性

冪處的和函数在其收敛域内是连续的。这意味着，如果一个幂级数在某个区间内收敛，那么这个级数在这个区间内的和函数是连续的。

2.2 可积性

冪處的和函数在其收敛域内是可积的，可以通过逐项积分公式进行积分：

[ int0^x s(t)dt = sum{n=0}^{infty} frac{a_n}{n+1}x^{n+1} ]

逐项积分后所得到的幂级数与原级数有相同的收敛半径。

2.3 可导性

冪處和函数在其收敛区间内具有任意阶导数，并且可以通过逐项求导公式进行求导：

[ s'(x) = sum_{n=1}^{infty} na_nx^{n-1} ]

逐项求导后所得的幂级数与原级数有相同的收敛半径。

3. 函数的幂级数展开

给定一个函数，通常我们希望知道它是否可以在某个区间展开成幂级数。假设函数 (f(x)) 在某邻域内能展开成幂级数，则有：

[ f(x) = a_0 + a_1(x-x_0) + a_2(x-x_0)^2 + cdots ]

展开幂级数的过程可以用于解决复杂的数学问题，并且在数值计算中具有重要的应用价值。

4. 麦克劳林公式

麦克劳林公式是泰勒公式在 (x_0=0) 时的特殊情况。它用于在 (x=0) 附近，用一个多项式函数去近似一个复杂函数：

[ f(x) = f(0) + f'(0)x + frac{f”(0)}{2!}x^2 + cdots ]

该公式在数值分析中被广泛用于函数逼近。

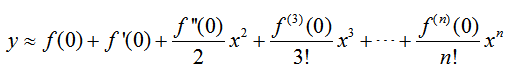
5. 泰勒公式

泰勒公式是麦克劳林公式的推广，它不局限于 (x_0=0)，而是在 (x_0) 处展开。其形式为：

[ f(x) = f(x_0) + f'(x_0)(x-x_0) + frac{f”(x_0)}{2!}(x-x_0)^2 + cdots ]

泰勒公式在工程学和物理学中具有重要的应用价值。

6. 冪處在数据分析中的应用

在统计学中，冪處常用于拟合数据分布。尤其在处理大数据或复杂数据集时，幂律分布（power-law distribution）是一种常用模型。

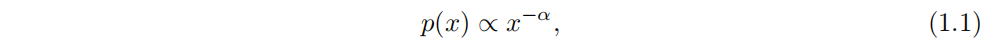
6.1 连续与离散幂律分布

幂律分布有连续和离散两种基本形式。连续幂律分布由概率密度 (p(x)) 描述，而离散幂律分布则关注于量只能取一组离散值的情况。

6.2 幂律分布的拟合

在处理幂律分布时，极大似然估计法是常用的参数化方法。此方法可以有效估计尺度参数 (alpha) 和数据的幂律行为的下界。

7. 冪處的未来研究与发展

随着科学和工程技术的发展，冪處在数学、物理、工程和数据科学等领域中的应用将变得更加广泛。未来的研究可能集中在提高幂级数的计算效率、优化其在大数据分析中的应用等。

结论

冪處作为数学分析中的一个基本工具，其广泛的应用和重要的性质使其成为数学研究和应用中的一个重要领域。通过对冪處的深入理解，我们可以更好地解决复杂的数学问题，提升科学研究的深度和广度。

FAQ

1. 问：什么是冪處？

   • 答：冪處是以无穷级数形式表示的函数，其中每一项都是幂函数乘以常数，用于表示和逼近复杂函数。

2. 问：冪處有哪些应用？

   • 答：冪處广泛应用于数学分析、物理学、工程学和数据科学等领域，用于函数逼近、数据拟合等。

3. 问：如何判断一个函数能否展开成冪處？

   • 答：通常通过泰勒公式和麦克劳林公式判断函数在某个区间内是否可以展开成幂级数。

4. 问：什么是幂律分布？

   • 答：幂律分布是指其概率分布的尾部遵循幂律的一种分布形式，常用于描述自然和社会现象。

5. 问：泰勒公式与麦克劳林公式有何区别？

   • 答：麦克劳林公式是泰勒公式在 (x_0=0) 时的特殊情况，泰勒公式更为一般，适用于任何 (x_0)。