Log函数及其运算法则

对数的起源与定义

对数（logarithm）的概念源于指数函数，是指数函数的反函数。具体来说，若有关系式 $y = a^x$，则可以通过对数变换表示为 $x = log_a y$。这里，$a$ 是对数的底，$y$ 是真数，而 $x$ 是结果。通常，底数 $a$ 必须大于零且不等于一。

对数的表示形式

1. 常用对数：以 10 为底的对数记作 $lg N = log_{10} N$。
2. 自然对数：以无理数 e（约等于 2.71828）为底的对数记作 $ln N = log_e N$。自然对数在数学和科学计算中有广泛应用。
3. 一般对数：以任意正数 $a$ 为底的对数，表示为 $log_a N$。

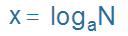
对数函数的性质

对数函数是指形如 $y = log_a x$ 的函数，其中 $x$ 是自变量。对数函数具有以下基本性质：

函数的定义域

对数函数的定义域为所有正实数，即 $x > 0$。这是因为对数仅对正数有意义，负数和零没有对数。

函数的基本性质

1. 过定点：当 $x = 1$ 时，$y = log_a 1 = 0$。
2. 单调性：
   • 当 $a > 1$ 时，$log_a x$ 是增函数。
   • 当 $0 < a < 1$ 时，$log_a x$ 是减函数。

对数运算法则

对数的运算遵循几条重要的法则，这些法则与指数运算密切相关：

积的对数

两个正数的积的对数等于它们对数的和：

$$ log_a (MN) = log_a M + log_a N $$

商的对数

两个正数商的对数等于它们对数的差：

$$ log_a left( frac{M}{N} right) = log_a M – log_a N $$

幂的对数

一个正数幂的对数等于幂的指数乘以底数的对数：

$$ log_a (M^p) = p cdot log_a M $$

对数公式的推导

对数公式的推导是理解对数运算的关键。以下是常见对数恒等式及其证明：

恒等式

对于 $a^t = N$，其中 $a > 0$ 且 $a neq 1$，有恒等式：

$$ a^{log_a N} = N $$

证明

设 $log_a N = t$，则 $a^t = N$，从而有 $a^{log_a N} = a^t = N$，证明完毕。

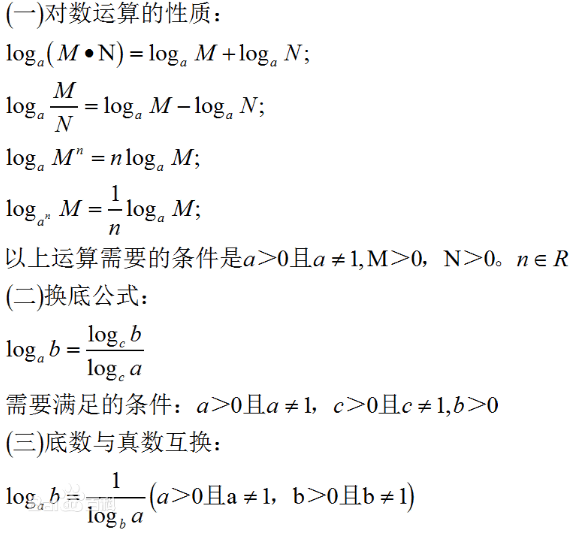
对数的实际应用

在实际应用中，对数具有广泛的应用场景，包括科学计算、工程领域、金融分析等。以下是对数在一些实际场景中的应用：

科学计算中的应用

对数在科学计算中常用于处理指数增长的现象，例如细胞分裂、放射性衰变等。自然对数 $e$ 作为增长率的极限值，在描述连续增长过程时尤为重要。

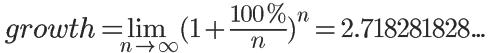
金融领域中的应用

在金融领域，对数常用于计算复利、评估股票增长率等。对数能够简化复杂的指数计算，使得金融分析更为直观。

对数的误区与注意事项

虽然对数在数学中是一个强有力的工具，但在使用过程中仍需注意一些常见误区：

负数与零无对数

在实数范围内，负数和零没有对数。这是因为对数函数的定义域仅限于正数。

虚数范围内的对数

在虚数范围内，负数是有对数的，但这涉及到复数对数的概念，与实数对数不同。

代码示例：对数运算实现

为了更好地理解对数的运算，我们可以通过编程来实现对数运算的基本规则。

import math

def log_operations(base, number):
    # 计算对数
    log_value = math.log(number, base)
    return log_value

result = log_operations(10, 100)
print(f"log_10(100) = {result}")

FAQ

什么是对数？

对数是指数函数的反函数，用于表示一个数是底数的多少次幂。

对数有什么实际应用？

对数在科学计算、金融分析和工程领域中有广泛应用，常用于处理指数增长问题。

为什么负数没有对数？

在实数范围内，负数没有对数，因为对数函数的定义域仅限于正数。

什么是自然对数？

自然对数是以无理数 e 为底的对数，常用于描述自然界中的连续增长现象。

如何计算对数运算？

对数运算可以通过积、商、幂的对数公式进行计算，也可以使用编程语言中的对数函数实现。