大数定理：概率与统计的基石

大数定理是概率论中一个核心的定理，它揭示了在大量随机事件的重复实验中，事件频率如何收敛于事件的概率。本文将深入探讨大数定理的各种形式，包括伯努利大数定律、辛钦大数定律和切比雪夫大数定律，以及中心极限定理的应用。通过对这些定理的详细分析，我们将理解大数定理在统计学和概率论中的重要性。

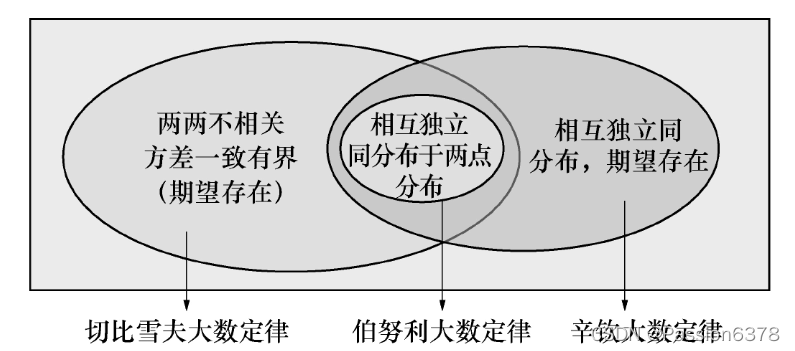
伯努利大数定律

伯努利大数定律是大数定理的最基本形式，适用于二项分布的情形。设进行$n$次独立实验，$n_A$为事件发生的次数，$p$为事件发生的概率，则对于任意$orall epsilon>0$，有：

$$
limlimits_{ntoinfty} Pleft(left|frac{n_A}{n}-pright|< epsilonright) = 1
$$

这表明随机事件A在$n$次试验中发生的频率会以概率收敛于$p$。随着实验次数的增加，事件发生的频率会无限接近于事件的概率。

伯努利大数定律示意图

辛钦大数定律

辛钦大数定律适用于更广泛的情形，即随机变量独立同分布且具有相同的数学期望$mu$。对于$n$个独立同分布的随机变量$X_1, X_2,…X_n$，有：

$$
limlimits_{ntoinfty} Pleft(left|frac{Sigma_1^nX_k}{n}-muright|< epsilonright) = 1
$$

这表明，随着观察次数的增加，样本平均值将趋近于期望值。这是用算术平均值计算期望的理论基础。

辛钦大数定律图示

切比雪夫大数定律

切比雪夫大数定律适用于方差有限的随机变量序列。设随机变量序列$X_1, X_2,…X_n$，它们两两不相关，且方差存在并有共同上界，则：

$$
limlimits_{ntoinfty} Pleft(left|frac{Sigma_1^nX_k-Sigma_1^nmu_k}{n}right|< epsilonright) = 1
$$

这个定理不要求随机变量同分布，但对方差有较高的要求。它通过样本平均数估计总体平均数提供了理论支持。

切比雪夫大数定律示意图

独立同分布的中心极限定理

中心极限定理则探讨了独立同分布随机变量序列的标准化和正态分布的关系。假设随机变量序列$X_1, X_2,…X_n$独立同分布，且期望$
mu$和方差$sigma^2$存在，那么：

$$
limlimits_{ntoinfty} Pleft(frac{Sigma_1^nX_k-nmu}{sqrt{n}sigma}le xright) = Phi(x)
$$

其中$Phi(x)$为标准正态分布函数。这意味着无论原始分布如何，足够多的独立同分布变量的和经过适当标准化后会趋向正态分布。

中心极限定理图示

大数定理的实际应用

在统计学中，大数定理提供了抽样理论的基础。它帮助我们理解样本平均如何反映总体平均，并在金融、物理、社会科学等领域广泛应用。例如，在金融市场中，投资者利用大数定理来分析股票回报的长期平均趋势。

示例：骰子掷投实验

通过一个简单的骰子掷投实验，我们可以直观理解大数定理。假设我们连续投掷一个均匀的六面骰子，期望值为3.5。根据大数定理，随着投掷次数的增加，平均值应趋近于3.5。

clear all;
clf;
clc;
num_trials = 1000;
trials = randi(6, [1 num_trials]);
figure(1);
plot(cumsum(trials)./(1:num_trials), 'r-');
hold on;
plot([1 num_trials], [3.5 3.5], 'color', [0 0.5 0]);
title('average dice value against number of rolls');
xlabel('trials');
ylabel('mean value');
legend('average', 'y=3.5');
axis([0 num_trials 1 6]);

骰子掷投实验图示