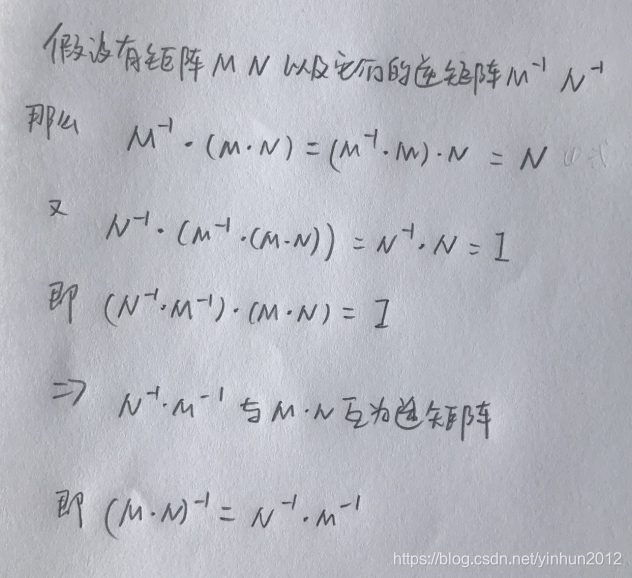常见矩阵的逆矩阵求解方法

在数学和计算中，矩阵的逆矩阵是一个重要的概念，特别是在线性代数和计算机图形学中。本文探讨了几种常见的矩阵逆矩阵求解方法，包括待定系数法、伴随矩阵法和初等变换法。这些方法不仅在理论上具有重要意义，也在实际应用中被广泛使用，如在三维图形学中，实现坐标变换的逆运算。通过理解这些逆矩阵的运算性质和推导过程，可以为后续的复杂计算提供坚实的数学基础。

待定系数法求逆矩阵

方法概述

待定系数法是一种通过假设逆矩阵的元素，然后通过方程组求解来找到逆矩阵的方法。对于给定的矩阵 ( A )，我们假设其逆矩阵 ( A^{-1} ) 的形式，然后通过解方程组求出具体的元素值。

具体步骤

设矩阵 ( A ) 为：

1, 2

-1, -3

假设逆矩阵 ( A^{-1} ) 为：

a, b

c, d

根据矩阵乘法的定义，我们可以得到以下方程组：

a + 2c = 1

b + 2d = 0

-a - 3c = 0

-b - 3d = 1

解得 ( a = 3 ), ( b = 2 ), ( c = -1 ), ( d = -1 )。

示例应用

此方法适用于小型矩阵的手动计算，可以有效地帮助理解逆矩阵的求解过程。

伴随矩阵法求逆矩阵

方法概述

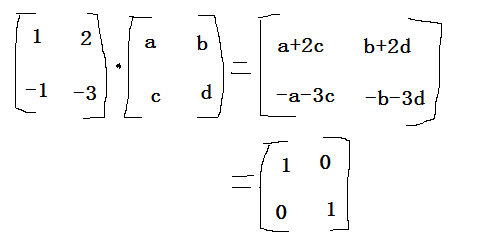
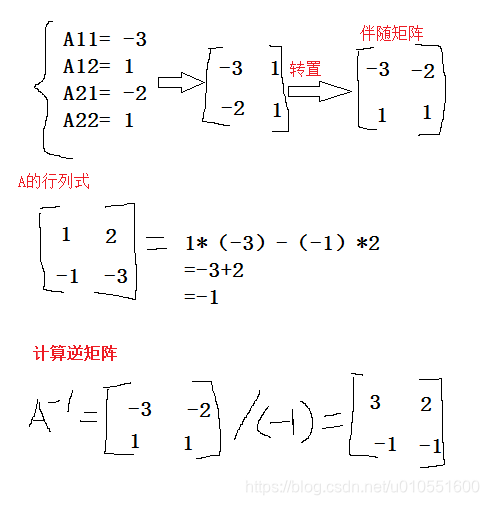
伴随矩阵法是一种利用矩阵的伴随矩阵和行列式来求逆矩阵的方法。通过计算伴随矩阵，再除以行列式，便可以得到逆矩阵。

具体步骤

设矩阵 ( A ) 为：

1, 2

-1, -3

其伴随矩阵 ( A^* ) 为：

-3, -2

1, 1

行列式 ( |A| ) 为：

1*(-3) - (-1)*2 = -1

因此，逆矩阵 ( A^{-1} = frac{A^}{|A|} = -A^ ) 为：

3, 2

-1, -1

示例应用

此方法适用于较小且计算复杂度不高的矩阵，尤其是在确定行列式不为零时。

初等变换法求逆矩阵

方法概述

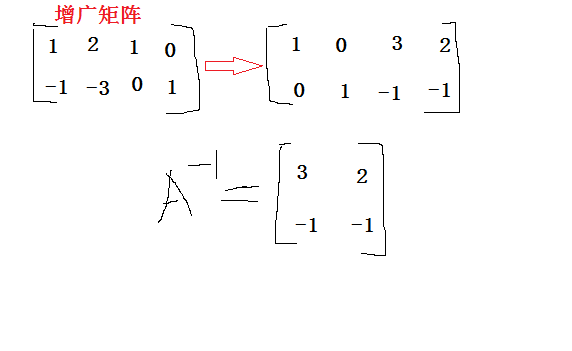
初等变换法通过将矩阵转换为单位矩阵，同时对单位矩阵进行相同的初等变换，从而得到逆矩阵。

具体步骤

首先写出增广矩阵 ( A|I ) ：

1 2 1 0

-1 -3 0 1

然后进行一系列初等行变换：

1. 第1行加到第2行：

1 2 1 0

0 -1 1 1

2. 第2行 ( times 2 ) 加到第1行：

1 0 3 2

0 -1 1 1

3. 第2行 ( times (-1) )：

1 0 3 2

0 1 -1 -1

示例应用

此方法适用于通过一系列行操作求逆的情况，特别是在进行矩阵变换时。

转置矩阵的定义与性质

转置矩阵定义

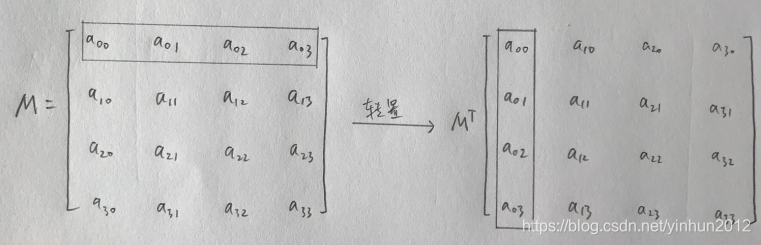
转置矩阵是通过将矩阵的行和列互换得到的新矩阵。对于矩阵 ( A ) 的转置，记为 ( A^T )。

运算性质

转置矩阵的行列式值不变。以下是其运算性质：

1. ( (A^T)^T = A )
2. ( (A + B)^T = A^T + B^T )
3. ( (AB)^T = B^T A^T )

应用

转置矩阵在矩阵运算中经常被使用，尤其是在线性代数和几何变换中。

逆矩阵的定义与用途

逆矩阵定义

逆矩阵是指矩阵 ( A ) 存在一个矩阵 ( A^{-1} )，使得 ( A times A^{-1} = I )，其中 ( I ) 为单位矩阵。

用途

逆矩阵常用于求解线性方程组、矩阵变换中的逆变换以及图形学中的几何变换。

应用实例

在三维图形学中，逆矩阵用于将变换后的坐标还原到原始坐标。

逆矩阵的运算性质

性质概述

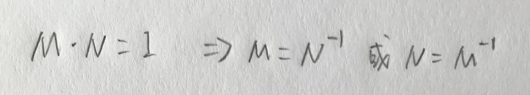
逆矩阵具有多种运算性质，使得复杂的矩阵运算得以简化和统一。

具体性质

1. ( (A^{-1})^{-1} = A )
2. ( (AB)^{-1} = B^{-1} A^{-1} )
3. ( (A^T)^{-1} = (A^{-1})^T )

应用

这些性质在矩阵的组合运算、变换和求解中具有重要作用。

矩阵逆运算在三维图形学中的应用

应用场景

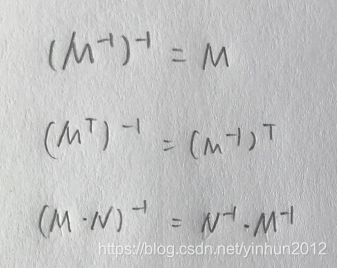
在三维图形学中，矩阵逆运算用于变换坐标系、计算光影效果等。

实际应用

通过逆矩阵，可以将物体从世界坐标系转换回局部坐标系，实现物体的旋转、缩放和移动的逆变换。

实例分析

在着色器编程中，逆矩阵用于计算光源位置和观察位置的变换。

FAQ

问：什么是待定系数法求逆矩阵？

• 答：待定系数法是一种通过假设逆矩阵的元素，然后通过方程组求解来找到逆矩阵的方法。对于给定的矩阵，我们假设其逆矩阵的形式，然后通过解方程组求出具体的元素值。这种方法适用于小型矩阵的手动计算。

问：伴随矩阵法是如何求逆矩阵的？

• 答：伴随矩阵法求逆矩阵是通过计算矩阵的伴随矩阵，然后除以矩阵的行列式得到逆矩阵。具体而言，对于矩阵 ( A )，首先计算其伴随矩阵 ( A^ )，然后计算行列式 ( |A| )，逆矩阵 ( A^{-1} = frac{A^}{|A|} )。

问：初等变换法求逆矩阵的步骤是什么？

• 答：初等变换法求逆矩阵的步骤包括：首先构建增广矩阵 ( A|I )，然后通过一系列初等行变换将矩阵 ( A ) 转换为单位矩阵，同时对单位矩阵进行相同的变换。最终，单位矩阵右侧的部分即为逆矩阵。

问：逆矩阵在三维图形学中的应用有哪些？

• 答：在三维图形学中，逆矩阵用于变换坐标系和计算光影效果等。例如，通过逆矩阵，可以将物体从世界坐标系转换回局部坐标系，实现旋转、缩放和移动的逆变换。在着色器编程中，逆矩阵常用于计算光源位置和观察位置的变换。

问：常见矩阵的逆矩阵有哪些运算性质？

• 答：常见矩阵的逆矩阵运算性质包括：( (A^{-1})^{-1} = A )，( (AB)^{-1} = B^{-1} A^{-1} )，以及 ( (A^T)^{-1} = (A^{-1})^T )。这些性质在矩阵的组合运算、变换和求解中非常重要。