信息熵及其在决策树中的应用

信息熵，一个源自信息论的重要概念，在数据科学和机器学习领域中扮演着关键角色。本文将深入探讨信息熵的含义、计算方法及其在决策树，尤其是ID3和C4.5算法中的应用，并分析信息增益和信息增益率这两个核心概念。

信息熵的定义与理解

熵的起源

熵，最初在物理学中用来描述系统的无序程度。香农在其1948年的论文《通讯的数学理论》中引入了信息熵的概念，用以衡量信息的不确定性。在信息论中，熵被定义为接收的每条消息中包含的信息的平均量，也称为信息熵或信源熵。

信息熵的计算

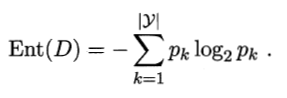
信息熵是度量样本集合纯度的常用指标。如果样本集合D中第k类样本所占的比例为p_k，则D的信息熵定义为：

Ent(D) = -∑(p_k * log2(p_k))

熵的物理意义

熵值越小，表示样本集合的纯度越高；熵值越大，表示样本集合的不确定性越高。

信息熵在决策树中的应用

决策树中的信息熵

决策树算法中，信息熵被用来选择最优的属性进行节点划分。ID3算法利用信息增益进行计算，而C4.5算法则使用增益率。

信息增益的计算

信息增益是特征选择的一个重要指标，定义为特征划分数据集前后熵的差值。

Gain(D, a) = Ent(D) - ∑(|Dv|/|D| * Ent(Dv))

信息增益率

信息增益率是C4.5算法中使用的一个概念，用于减少信息增益对属性取值数目的偏好。

GainRatio(D, a) = Gain(D, a) / Inv(a)

其中，Inv(a)是属性a的固有熵。

信息熵的实际案例分析

决策树案例分析

通过计算信息增益，我们可以分析出不同特征对决策树分类结果的影响。例如，通过性别和活跃度两个特征，我们可以判断哪个特征对用户流失影响更大。

信息增益的实际计算

以下是对性别和活跃度特征的信息增益计算：

Gain(D, 性别) = 0.0064

Gain(D, 活跃度) = 0.6776

从计算结果可以看出，活跃度的信息增益远大于性别，说明活跃度对用户流失的影响更大。

FAQ

1. 问：信息熵在决策树中的作用是什么？
   答：信息熵在决策树中用于衡量样本集合的纯度，帮助选择最优的属性进行节点划分。

2. 问：信息增益和信息增益率有什么区别？
   答：信息增益衡量特征划分数据集前后熵的差值，而信息增益率则进一步考虑了属性的固有熵，减少了对属性取值数目的偏好。

3. 问：为什么活跃度的信息增益会比性别的大？
   答：活跃度的特征变化对分类结果的影响更大，因此其信息增益也更大，表明活跃度是影响用户流失的一个更重要的特征。

4. 问：如何计算信息熵？
   答：信息熵的计算公式为Ent(D) = -∑(p_k * log2(p_k))，其中p_k是样本集合中第k类样本所占的比例。

5. 问：信息熵的值越小意味着什么？
   答：信息熵的值越小，表示样本集合的纯度越高，不确定性越低。

通过本文的探讨，我们深入了解了信息熵的概念、计算方法及其在决策树中的应用，希望能够帮助读者更好地理解和运用这一重要的信息论概念。