对数函数的深入探讨与应用

对数的起源与定义

对数源于指数，是指数函数的反函数。在数学中，指数和对数是互为反函数的关系。具体来说，如果我们有一个方程 y = a^x，那么 x 就是以 a 为底的 y 的对数，记作 x = log_a(y)。这种关系不仅在数学理论中至关重要，在计算与工程中也有广泛的应用。

对数的定义详细解析：

在数学定义中，如果 N = a^x 且 a > 0 且 a ≠ 1，那么 x 就是以 a 为底 N 的对数，记作 x = log_a(N)。其中，a 被称为底数，N 被称为真数，x 则是“以 a 为底 N 的对数”。

对数的表示及性质

1. 以 a 为底 N 的对数记作 log_a(N)。
2. 以 10 为底的对数，常被称为常用对数，记作 lg(N) = log_10(N)。
3. 以无理数 e（约等于 2.71828）为底的对数称为自然对数，记作 ln(N) = log_e(N)。
4. 零没有对数。
5. 在实数范围内，负数无对数，但在虚数范围内，负数是有对数的。

对数函数的定义与性质

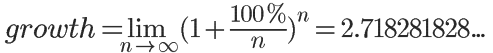
对数函数是通过对数的定义而形成的一个函数。在数学表达式中，函数 y = log_a(x) 被称为对数函数，其中 x 是自变量。对数函数的定义域是 x > 0。

对数函数的基本性质

1. 对数函数过定点 (1, 0)，即当 x = 1 时，y = 0。
2. 当 0 < a < 1 时，在 x > 0 上是减函数；
3. 当 a > 1 时，在 x > 0 上是增函数。

对数运算法则

对数运算法则是一种特殊的运算方法，用于处理积、商、幂、方根的运算。通过指数和对数的相互转化，我们可以得到以下运算规则：

对数运算的基本规则

1. 两个正数的积的对数，等于这两个数的对数的和：

   log_a(MN) = log_a(M) + log_a(N)

   

2. 两个正数商的对数，等于被除数的对数减去除数对数的差：

   log_a(M/N) = log_a(M) – log_a(N)

   

3. 一个正数幂的对数，等于幂的底数的对数乘以幂的指数：

   log_a(M^n) = n * log_a(M)

   

4. 一个正数的算术根的对数，等于被开方数的对数除以根指数：

   log_a(√M) = (1/2) * log_a(M)

   

对数公式与推导

对数公式基本知识

1. log_a(1) = 0
2. log_a(a) = 1
3. 对数的负数和零无定义。
4. log_a(a^n) = n
5. a^log_a(N) = N

对数恒等式及其证明

在数学中，一个重要的对数恒等式是 a^log_a(N) = N。这一公式的推导如下：

设 log_a(N) = t，那么根据对数的定义，我们有 a^t = N。因此，a^log_a(N) = a^t = N。由此证明了该恒等式的正确性。

对数在实际中的应用

自然对数与增长率

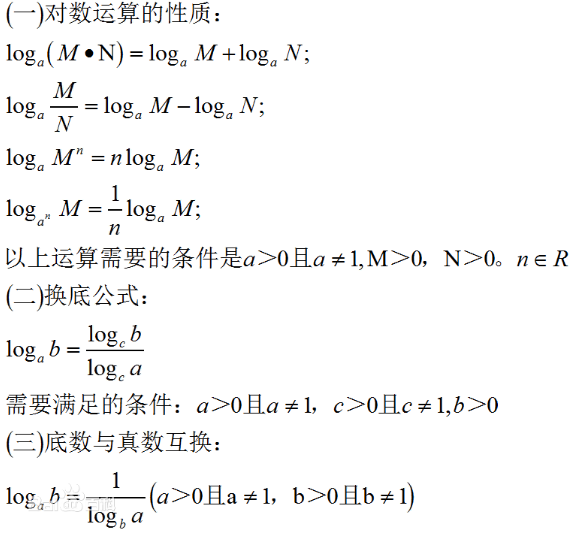
自然对数的底数 e 是一个重要的数学常数，约为 2.71828。其在自然现象中的应用非常广泛，例如在细胞分裂的模型中，e 描述了在单位时间内持续的增长可以达到的极限。

代码中的对数应用

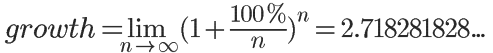
在编程中，对数函数被广泛应用于算法的复杂度分析、数据的对数变换等场景。例如，Python 中的 math 库提供了对数函数，可以用于计算对数。

import math

print(math.log(10))  # 输出为 2.302585092994046

print(math.log10(10))  # 输出为 1.0

结论

对数函数在数学和实际应用中都扮演着重要的角色。通过了解对数的基本定义、性质和运算法则，我们可以更好地应用对数来解决复杂的数学问题和实际工程问题。

FAQ

1. 问：对数函数的定义域是什么？

   • 答：对数函数的定义域是所有大于零的实数，即 x > 0。

2. 问：自然对数的底数 e 有什么实际意义？

   • 答：自然对数的底数 e 描述了在单位时间内持续增长的极限值，常用于描述自然增长过程，如细胞分裂。

3. 问：在编程中如何使用对数函数？

   • 答：在编程中，可以使用 Python 的 math 库中的 log 函数来计算对数。