反函数的深入探讨与应用

反函数的定义与特性

在数学中，反函数是一个非常重要的概念。反函数是指对于一个给定的函数y=f(x)，存在另一个函数g(y)使得g(f(x))=x对所有x在f的定义域内都成立。换句话说，反函数是原函数的一个“逆操作”，它能够将函数的输出值映射回输入值。

反函数的存在条件

要确定一个函数是否有反函数，必须检查该函数是否是一一对应的。这意味着对于定义域中的每一个输入x，都有唯一的输出y，反之亦然。只有满足这个条件的函数才被称为单值函数，并且拥有反函数。

反函数的图像特征

函数f(x)与其反函数f^(-1)(x)的图像有一个显著的特征：它们关于直线y=x对称。这种对称性是反函数图像识别的一个关键指标。

反函数的基本性质

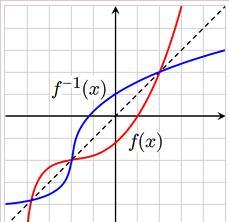
反函数的性质是理解和应用反函数的关键。以下是一些基本性质：

图像对称性

• 性质1：函数f(x)与它的反函数f^(-1)(x)图像关于直线y=x对称。

定义域与值域的关系

• 性质2：函数存在反函数的充要条件是，函数的定义域与值域是一一映射。

单调性一致性

• 性质3：一个函数与它的反函数在相应区间上单调性一致。

偶函数与奇函数的反函数

• 性质4：大部分偶函数不存在反函数，而奇函数不一定存在反函数，但如果存在，则其反函数也是奇函数。

连续函数的单调性

• 性质5：一段连续的函数的单调性在对应区间内具有一致性。

严格增（减）函数的反函数

• 性质6：严增（减）的函数一定有严格增（减）的反函数。

反函数的唯一性

• 性质7：反函数是相互的且具有唯一性。

对应法则的互逆性

• 性质8：定义域、值域相反对应法则互逆（三反）。

反函数的导数关系

• 性质9：如果x=f(y)在开区间I上严格单调，可导，且f'(y)≠0，那么它的反函数y=f^(-1)(x)在区间S={x|x=f(y),y∈I}内也可导，且满足特定的导数关系。

恒等函数的反函数

• 性质10：y=x的反函数是它本身。

反函数的计算与应用

计算反函数

在实际应用中，计算反函数通常涉及到解方程。给定一个函数y=f(x)，要找到它的反函数，我们需要解出x关于y的表达式，即x=g(y)。这个过程可能涉及到代数变换、因式分解、使用求根公式等数学技巧。

反函数在科学中的应用

反函数在科学和工程领域有着广泛的应用。例如，在物理学中，力和加速度的关系可以通过反函数来表达；在化学中，反应速率常数与反应物浓度的关系也可以用反函数来描述。

编程中的反函数

在编程语言中，反函数的概念也被广泛应用。例如，在数据库查询中，通过反函数可以快速从查询结果中恢复原始数据。

反函数的图像绘制

绘制反函数图像是理解反函数特性的一个重要手段。通过绘制原函数和反函数的图像，我们可以直观地看到它们关于直线y=x的对称性。

绘制步骤

绘制反函数图像的步骤通常包括：确定原函数的图像，然后找到关于直线y=x的对称点，最后连接这些点形成反函数的图像。

绘制工具

可以使用各种数学软件和编程语言来绘制反函数图像，例如MATLAB、Python的matplotlib库等。

import matplotlib.pyplot as plt
import numpy as np

def f(x):
    return x**2

def f_inverse(x):
    return np.sqrt(x)

x = np.linspace(-2, 2, 400)
y = f(x)
x_inverse = np.linspace(0, 4, 400)
y_inverse = f_inverse(x_inverse)

plt.figure(figsize=(8, 6))
plt.plot(x, y, label='f(x) = x^2')
plt.plot(x_inverse, y_inverse, label='f^(-1)(x) = sqrt(x)')
plt.plot(np.linspace(-2, 4, 10), np.linspace(-2, 4, 10), 'k--', label='y=x')
plt.legend()
plt.show()

图像分析

通过上述代码块，我们可以得到原函数f(x) = x^2和它的反函数f^(-1)(x) = sqrt(x)的图像，并观察到它们关于直线y=x的对称性。

反函数的导数计算

反函数的导数是微积分中的一个重要话题。如果函数f在某个区间上严格单调且可导，那么它的反函数在相应的区间上也可以导，并且它们的导数之间存在特定的关系。

导数关系式

如果x=f(y)在开区间I上严格单调，可导，且f'(y)≠0，那么它的反函数y=f^(-1)(x)在区间S={x|x=f(y),y∈I}内也可导，且满足以下关系式：

导数的几何意义

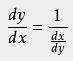
反函数的导数可以从几何上解释为曲线在该点处的切线的斜率的倒数。这意味着，如果原函数在某个点处的切线斜率较大，那么它的反函数在对应点处的切线斜率就较小。

导数的计算例子

考虑函数f(x) = x^3，我们要找到它的反函数的导数。首先，我们找到反函数f^(-1)(x) = x^(1/3)，然后计算其导数。

f^(-1)'(x) = (x^(1/3))' = 1/3 * x^(-2/3)

FAQ

问：什么是反函数？

答：反函数是一个函数，它能够将原函数的输出值映射回输入值，即如果y=f(x)，则x=f^(-1)(y)。

问：如何判断一个函数是否有反函数？

答：一个函数有反函数当且仅当它是一一对应的，即定义域中的每个输入都有唯一的输出，反之亦然。

问：反函数的图像有什么特点？

答：反函数的图像与原函数的图像关于直线y=x对称。

问：反函数在实际中有哪些应用？

答：反函数在科学、工程和编程中有广泛应用，例如在物理学中描述力和加速度的关系，在数据库查询中恢复原始数据等。

问：如何计算反函数的导数？

答：如果x=f(y)在某个区间上严格单调且可导，那么它的反函数y=f^(-1)(x)在相应的区间上也可导，并且它们的导数之间存在特定的关系。