深入探讨卷积的物理意义与应用

卷积是数学、信号处理和计算机科学中的一个核心概念，它在理论和应用中都起到了重要的作用。虽然卷积常常被应用于复杂的数学和工程问题中，但它的基本原理却可以通过简单的例子来理解。本文将通过多角度的分析与讲解，帮助读者全面理解卷积的意义、数学定义及其在实际中的应用。

什么是卷积

卷积可以被简单地理解为两个函数之间的运算，它通过对一个函数进行加权叠加，从而得到另一个函数的响应。这种运算在处理信号和图像时尤为重要，因为它可以通过对输入信号进行卷积操作，获取系统的输出响应。

卷积在数学上被定义为两个函数 f 和 g 的积分或和，表示为 (f∗g)(t) = ∫ f(τ)g(t−τ)dτ。在离散情况下，卷积被定义为一个和式。这种运算具有线性和时不变的特性，意味着卷积的结果只与输入信号的形状和卷积核有关，而不依赖于信号的具体位置或时间。

数学定义的卷积

卷积的基本原理可以通过信号处理中的简单例子来说明。假设有两个离散信号 x[n] 和 y[n]，卷积的过程相当于对信号 x[n] 进行“翻转”并沿着 y[n] 移动，每一个位置上对两个信号进行相乘并累加。这个过程的结果就是两个信号的卷积。

在图像处理中，卷积常用于平滑、边缘检测等操作。通过一个卷积核（也被称为滤波器或模板），对图像进行卷积处理，可以有效地去除噪声或增强特定的图像特征。

离散卷积的一个简单实例是通过抛掷骰子来理解。假设有两枚骰子，每个骰子的点数分布可以用概率密度函数表示。将两个骰子的点数相加的概率可以通过卷积来计算。

骰子概率分布

这种模型可以帮助理解卷积在计算不同独立事件的联合概率分布时的应用。

卷积在信号处理中的一个重要应用是信号的滤波。通过卷积运算，能够对输入信号进行各种滤波处理，如低通滤波、高通滤波等。滤波的核心思想是通过卷积核对信号进行加权求和，从而消除或增强特定频率的成分。

信号滤波的基本原理是通过卷积核对输入信号进行加权求和。例如，一个简单的低通滤波器可以通过一个矩形卷积核实现，它能够消除信号中的高频成分，保留低频成分。

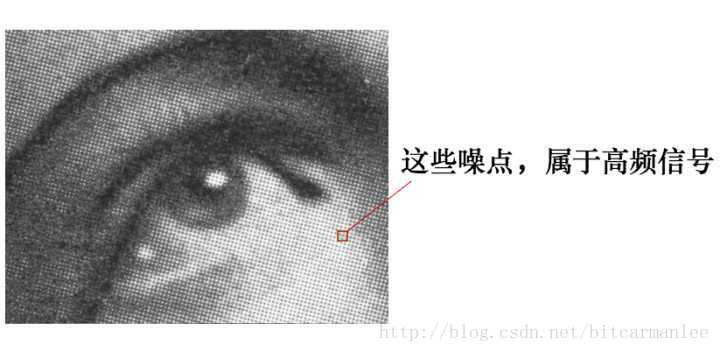
在图像处理中，滤波也可以通过卷积来实现。例如，利用卷积核可以平滑图像，去除图像中的噪声，或者通过边缘检测滤波器来增强边缘特征。

图像滤波

在深度学习中，卷积神经网络（CNN）是卷积应用的一个重要领域。CNN 利用卷积层来提取图像的特征，从而实现对图像的分类、检测等任务。卷积层通过多个卷积核对输入图像进行卷积操作，提取不同层次的特征。

卷积神经网络的工作原理是通过多个卷积层、池化层和全连接层的组合，实现对图像的特征提取和分类。卷积层通过卷积核对输入图像进行处理，提取特征，而池化层则通过降采样减少数据量和计算量。

这种结构使得 CNN 能够有效地处理大规模图像数据，并实现高精度的图像分类和识别。

卷积神经网络

卷积不仅在数学上有着重要的意义，在物理中也有广泛的应用。例如，在物理系统中，卷积可以用来描述一个系统的冲激响应，即系统对一个输入信号的响应。

在物理系统中，卷积可以用来求解线性时不变系统的响应。通过系统的冲激响应和输入信号的卷积，可以得到系统的输出信号。这一特性使得卷积在信号处理、控制工程等领域有着重要的应用。

计算卷积的方法有多种，包括直接计算法、快速傅里叶变换（FFT）法等。直接计算法是通过卷积的定义逐项计算，而 FFT 法则通过将卷积运算转化为频域中的乘法，从而提高计算效率。

快速傅里叶变换法是一种利用离散傅里叶变换（DFT）计算卷积的方法。通过将卷积运算转化为频域中的乘法，FFT 法可以大大提高计算效率，尤其适用于大规模数据的卷积计算。

这种方法在计算机视觉、信号处理等领域得到了广泛应用。

问：卷积在图像处理中有什么应用？
- 答：卷积在图像处理中用于滤波、边缘检测、特征提取等操作。通过卷积核对图像进行卷积，可以去除噪声或增强图像的特征。
问：卷积神经网络如何应用卷积？
- 答：卷积神经网络通过卷积层提取图像特征。卷积层利用多个卷积核对输入图像进行卷积，提取不同层次的特征，实现图像的分类和识别。
问：卷积的数学定义是什么？
- 答：卷积的数学定义是两个函数的积分或和。对于连续函数，卷积表示为(f∗g)(t) = ∫ f(τ)g(t−τ)dτ；对于离散函数，卷积表示为一个和式。
问：卷积的物理意义是什么？
- 答：卷积在物理中用于描述系统的冲激响应，即系统对输入信号的响应。通过卷积运算可以求解线性时不变系统的输出信号。
问：如何提高卷积计算的效率？
- 答：提高卷积计算效率的方法包括使用快速傅里叶变换（FFT）法和优化卷积核的设计等。FFT 法通过将卷积运算转化为频域中的乘法，可以显著提高计算效率。