深入探讨Lasso回归及其应用

Lasso回归，全称为最小绝对值收缩与选择算子回归，是一种用于特征选择和模型简化的线性回归方法。本文将详细探讨Lasso回归的原理、实现及其在数据科学中的应用。

1. Lasso回归的基本原理

Lasso回归通过在标准线性回归的损失函数中加入L1正则化项，迫使某些回归系数缩小到零。其数学表达式如下：

[J = frac{1}{n}sum_{i = 1}^n (f(bm x_i) – y_i)^2 + lambda |w|_1]

其中，(lambda) 是正则化参数，控制正则化的强度。L1正则化项是所有系数绝对值之和，能够有效地进行特征选择。

1.1 L1正则化的作用

L1正则化的主要作用是通过增加损失函数的惩罚项，减少模型的复杂度。这种方法尤其适合于高维数据集，因为它可以自动选择出最重要的特征，忽略不重要的特征。

1.2 Lasso回归与岭回归的区别

虽然Lasso回归和岭回归都属于正则化回归方法，但二者在正则化项上有所不同。岭回归使用L2正则化，导致系数趋近于零但不为零，而Lasso回归则通过L1正则化将一些系数直接压缩为零。

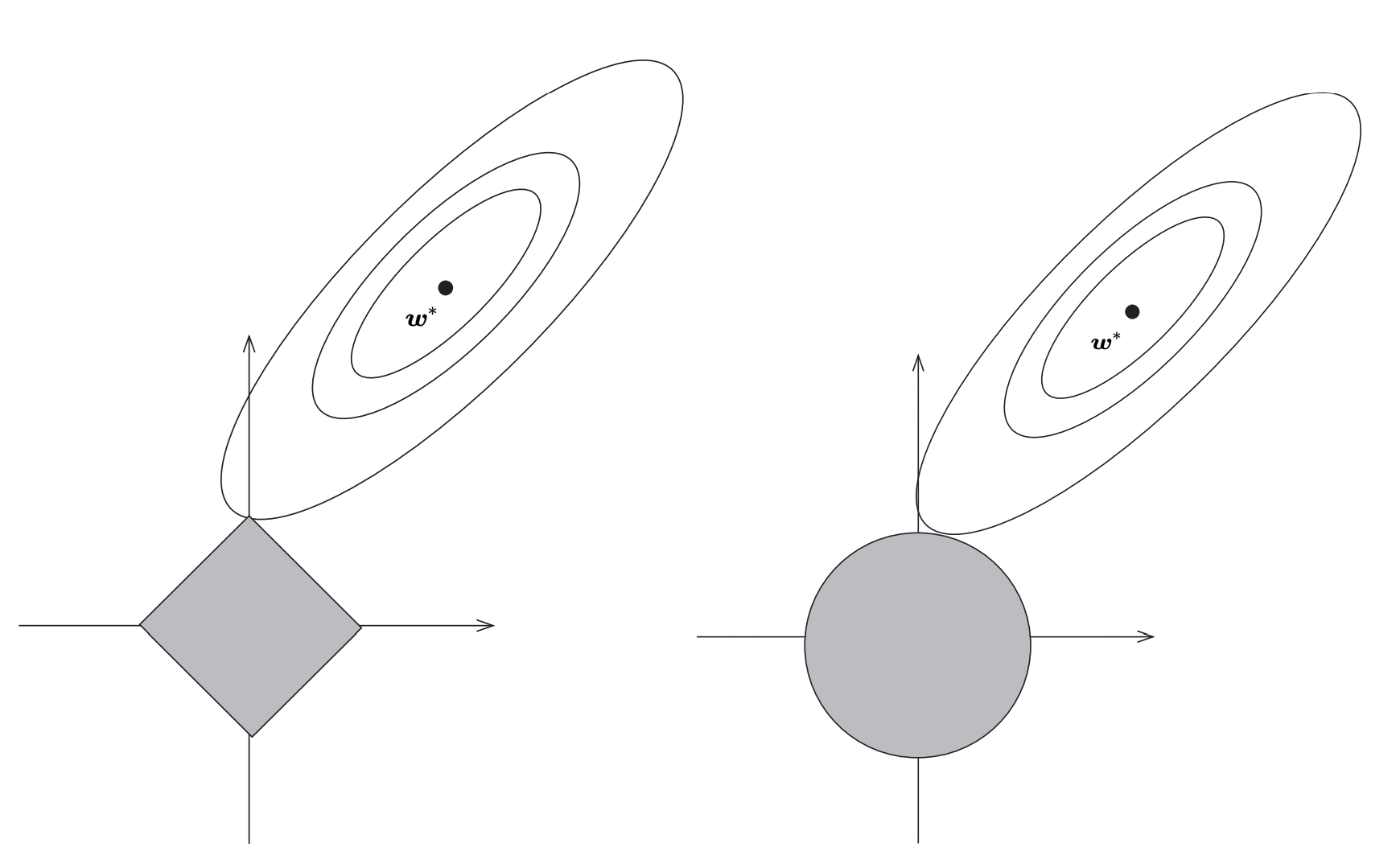
Lasso与岭回归比较图

2. Lasso回归的实现

Lasso回归的实现可以通过不同的算法实现，包括坐标下降法和最小角回归法。这些方法都能有效地计算回归系数。

2.1 坐标下降法

坐标下降法是一种常用的优化算法，通过在每次迭代中固定其他变量，只对一个变量进行优化，从而逐步逼近最优解。其优点是实现简单，计算速度快。

import numpy as np
from sklearn.linear_model import Lasso

X = np.random.rand(100, 10)
y = np.random.rand(100)

lasso = Lasso(alpha=0.1)
lasso.fit(X, y)

w = lasso.coef_

2.2 最小角回归法

最小角回归法通过逐步逼近的方式，选择与当前残差相关性最大的特征，直到所有特征的相关性都被消除。该方法适合于处理高维数据。

3. Lasso回归的应用场景

Lasso回归在数据科学中的应用非常广泛，尤其在特征选择和模型简化方面表现突出。

3.1 特征选择

在具有大量特征的数据集中，Lasso回归能够自动选择出对模型最有影响的特征，从而提高模型的效率和准确性。

3.2 模型简化

通过将不重要的特征系数压缩为零，Lasso回归可以简化模型结构，降低模型的复杂度，这对于提高模型的可解释性和应用性尤为重要。

4. Lasso回归的优势与挑战

Lasso回归在处理高维数据和特征选择上有明显优势，但也存在一些挑战，如参数选择和计算复杂度问题。

4.1 参数选择

正则化参数 (lambda) 的选择对Lasso回归的效果有显著影响。一般通过交叉验证来确定最佳参数。

4.2 计算复杂度

虽然Lasso回归具有良好的特征选择能力，但在处理极高维数据或巨型数据集时，计算复杂度可能成为一个问题。

5. 结论

Lasso回归作为一种强大的特征选择工具，在数据科学中具有广泛的应用前景。通过合理选择正则化参数，Lasso回归能够有效地提高模型的预测能力和简化模型结构。

FAQ

问：Lasso回归与岭回归的主要区别是什么？
- 答：Lasso回归使用L1正则化，使某些回归系数缩小到零，实现特征选择；而岭回归使用L2正则化，系数趋近于零但不为零。
问：如何选择Lasso回归的正则化参数？
- 答：通常通过交叉验证来选择正则化参数，以确保模型的最佳性能。
问：Lasso回归适用于什么样的数据集？
- 答：Lasso回归适用于高维数据集，尤其是在特征数大于样本数的情况下，可以有效进行特征选择和简化模型。