**相关系数与回归系数的深度解析**

一、基本概念及背景

在统计学和数据科学领域，相关系数和回归系数是两个非常重要的概念。它们在数据分析中广泛应用，帮助我们理解两个或多个变量之间的关系。相关系数用于度量变量之间线性关系的强度，而回归系数则用于描述一个变量如何影响另一个变量的数值变化。理解这两个概念对于进行有效的数据分析和模型构建至关重要。

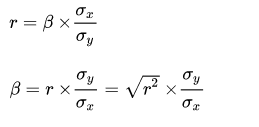
二、相关系数的定义与计算

1. 定义

相关系数，又称为Pearson相关系数，是一个用于衡量两个变量之间线性相关程度的量。其取值范围为[-1,1]，其中1表示完全正相关，-1表示完全负相关，0表示没有线性关系。

2. 计算公式

相关系数的计算公式为：

[
rho{xy} = frac{sum{i=1}^N (x_i – bar{x})(yi – bar{y})}{sqrt{sum{i=1}^N (xi – bar{x})^2} sqrt{sum{i=1}^N (y_i – bar{y})^2}}
]

该公式通过计算变量之间的协方差除以标准差的乘积，得出相关系数。

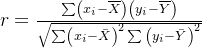
三、回归系数的定义与应用

1. 定义

回归系数是在回归方程中表示自变量对因变量影响大小的参数。它反映了自变量每变化一个单位，因变量平均变化的数量。回归系数可以是正数或负数，分别表示正向和负向影响。

2. 应用

回归系数在数据建模和预测中扮演着重要角色。通过对历史数据进行回归分析，可以预测未来数据的走势。回归分析广泛应用于经济预测、市场研究和科学研究等领域。

四、相关系数与回归系数的联系

1. 数学关系

在简单线性回归中，回归系数和相关系数之间存在如下关系：

[
r{xy} = rho{xy} cdot frac{sigma_y}{sigma_x}
]

其中，(r{xy})是回归系数，(rho{xy})是相关系数，(sigma_x)和(sigma_y)分别是自变量和因变量的标准差。

2. 实际应用

在实际应用中，相关系数可以帮助我们初步判断变量之间的关系，而回归系数则用于建立更精确的数学模型以进行预测。

五、相关系数与回归系数的区别

1. 含义上的区别

相关系数主要用于描述变量之间的相关程度，而回归系数则用于描述因变量如何随自变量变化。

2. 适用场景

相关系数通常用于初步分析和判断变量之间的关系，而回归系数则更多用于模型构建和预测分析。

六、相关系数与回归系数的计算实例

1. Python代码实例

以下是用Python计算相关系数和回归系数的示例代码：

import numpy as np
from scipy.stats import linregress

x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 5, 4, 5])

correlation_coefficient = np.corrcoef(x, y)[0, 1]
print(f"相关系数: {correlation_coefficient}")

slope, intercept, r_value, p_value, std_err = linregress(x, y)
print(f"回归系数: {slope}")

在这个代码块中，我们使用NumPy库计算相关系数，并使用SciPy库计算线性回归的回归系数。

七、总结与结论

通过本文的解析，我们可以清楚地看到相关系数和回归系数在数据分析中的重要作用。相关系数帮助我们理解变量间的关系，而回归系数则在预测模型中不可或缺。理解这两个概念及其应用，能够极大地提升数据分析的效率和准确性。

FAQ

1. 问：相关系数和回归系数可以相互替代吗？

• 答：不可以。相关系数用于描述变量之间的线性关系，而回归系数用于描述因变量受自变量影响的具体程度。

2. 问：如何选择使用相关系数还是回归系数？

• 答：如果需要了解变量之间的相关性，使用相关系数；如果需要建立预测模型和分析变量变化的影响，使用回归系数。

3. 问：相关系数为0时，回归系数一定为0吗？

• 答：不一定。相关系数为0仅表示没有线性关系，但可能存在非线性关系。

4. 问：在多元回归中，如何解释回归系数？

• 答：在多元回归中，回归系数表示在控制其他变量不变的情况下，自变量对因变量的影响。

5. 问：回归系数可以是负数吗？

• 答：可以。负数回归系数表示因变量随自变量的增加而减少，这表明两者存在负相关关系。