K-Means聚类算法是怎么发明的呢

K-Means算法的起源与发展

K-Means聚类算法最早可以追溯到1957年，由Hugo Steinhaus提出的想法。这一算法在1967年被James MacQueen正式命名为“k-means”。尽管如此，斯图亚特·劳埃德早在1957年就提出过类似的算法，这一算法在1982年由贝尔实验室正式发表。后来的Hartigan和Wong在1975年和1979年分别提出了更高效的版本，使得K-Means算法在处理大规模数据时变得更为可行。

K-Means算法的基本概念

K-Means算法是一种基于划分的聚类方法，旨在将n个对象划分为k个簇，以使簇内的对象具有更高的相似性。算法的核心思想是最小化每个数据点到其所属聚类中心的距离平方和。K-Means算法的基本步骤包括：

随机选择k个数据点作为初始聚类中心。
计算每个数据点到所有聚类中心的距离，并将其分配到最近的聚类中心。
重新计算每个聚类的中心点。
重复上述过程，直到聚类中心不再变化或达到预设的迭代次数。

K-Means算法的应用领域

K-Means算法因其简单快速的特点被广泛应用于各个领域。它适用于数据挖掘、模式识别、图像处理等场景。例如，在图像处理领域，K-Means可以用于图像的压缩和分割。在市场分析中，它可以帮助企业识别消费者群体的特征，以制定更有针对性的营销策略。此外，在社交网络分析中，K-Means可以用于发现用户间的社交圈和兴趣群体。

K-Means算法的优缺点分析

优点

简单易实现：K-Means算法的实现相对简单，适合快速开发和应用。
处理大数据集：算法复杂度为O(nkt)，适合处理大规模数据。
广泛应用：可应用于各种领域的聚类任务。

缺点

需要预先定义k值：用户必须事先确定聚类的数量k。
对初始值敏感：不同的初始中心选择可能导致不同的结果。
不适合非凸形状的簇：对非凸形状的数据集表现不佳。

K-Means的优化与变体

K-Means++

K-Means++算法通过改进初始聚类中心的选择，来提高算法的收敛速度和结果质量。其主要思想是在选择初始点时尽可能均匀地覆盖整个数据集，从而减少聚类迭代次数。

Elkan K-Means

Elkan K-Means通过减少不必要的距离计算来优化算法，利用三角不等式简化计算，显著提高了迭代速度。

Mini Batch K-Means

Mini Batch K-Means通过在每次迭代中仅使用一部分数据进行聚类，大大加快了处理速度，适用于大数据场景。

K-Means算法的实际应用示例

以下是一个使用Python实现K-Means聚类的简单示例代码：

import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans

X, y = make_blobs(n_samples=500, n_features=2, centers=4, random_state=42)

plt.scatter(X[:, 0], X[:, 1], c=y, alpha=0.5)
plt.title('Original Data')
plt.show()

kmeans = KMeans(n_clusters=4)
y_pred = kmeans.fit_predict(X)

plt.scatter(X[:, 0], X[:, 1], c=y_pred, alpha=0.5)
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1],
            c='red', marker='x', s=100, linewidths=3)
plt.title('K-Means Clustering Result')
plt.show()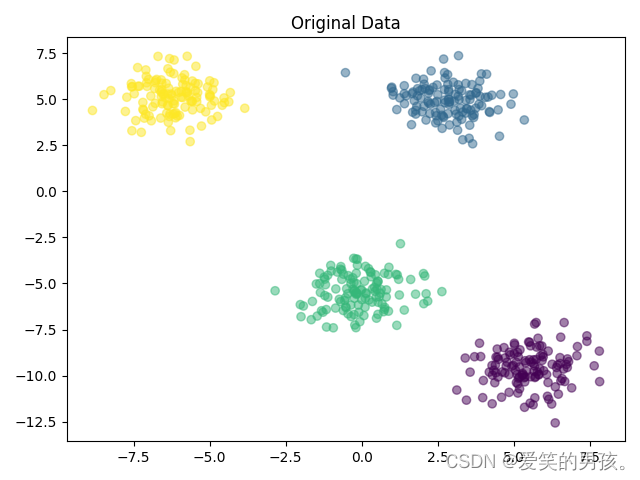

K-Means与KNN的区别

K-Means和KNN常被混淆，但它们在本质上是不同的。K-Means是一种无监督学习的聚类算法，而KNN是监督学习的分类算法。K-Means没有预定义的类别输出，而KNN需要分类标签。K-Means通过寻找最佳质心来划分数据，而KNN通过计算点与点之间的距离进行分类。

结论

K-Means算法以其简单高效的特性成为数据聚类的经典方法，广泛应用于各个领域。在实际应用中，了解其优缺点及优化策略可以帮助我们更好地利用这一算法。

FAQ

问：K-Means算法适用于哪些数据类型？
- 答：K-Means算法适用于数值型数据，但不适用于具有分类属性的数据。
问：如何选择K-Means中的k值？
- 答：常用的方法包括肘部法则（Elbow Method）和轮廓系数分析（Silhouette Analysis）来选择合适的k值。
问：K-Means算法如何处理离群点？
- 答：K-Means对离群点较为敏感，离群点可能会影响聚类结果。可以通过预处理数据或者使用更鲁棒的聚类算法来处理离群点。
问：K-Means可以用于非凸形数据吗？
- 答：K-Means适用于凸形数据，非凸形数据可能导致不理想的聚类结果，建议使用DBSCAN等算法。
问：K-Means算法的时间复杂度是多少？
- 答：K-Means算法的时间复杂度为O(nkt)，其中n为数据点数量，k为聚类数量，t为迭代次数。