梯度下降法详解及其在机器学习中的应用

梯度下降法（Gradient Descent）是机器学习中一种常用的优化算法，用于寻找目标函数的最小值。在机器学习模型的训练过程中，梯度下降法帮助调整模型参数以降低损失函数值，从而提高模型的预测准确性。本文将深入探讨梯度下降法的原理、变种、优缺点及其应用。

1. 什么是梯度下降法

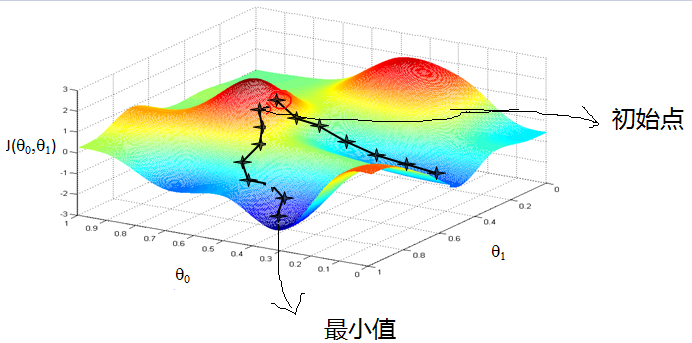
梯度下降法是一种求解无约束优化问题的迭代算法，主要用于找到某个函数的局部最小值。其基本思想是从一个初始点出发，沿着函数梯度的反方向进行迭代，以逐步逼近函数的极小值点。

1.1 梯度的概念

在数学上，梯度是一个向量，表示多元函数在某一点的变化率。对于函数 $f(x, y)$，梯度向量表示为 $(frac{partial f}{partial x}, frac{partial f}{partial y})$。梯度的方向即为函数增长最快的方向，而梯度的反方向则是函数下降最快的方向。

1.2 梯度下降法的原理

梯度下降法的原理在于通过多次迭代，沿着梯度的反方向移动，从而逐渐逼近目标函数的最小值。具体步骤如下：

初始化一个起始点 $theta_0$。
计算当前点的梯度 $nabla J(theta)$。
更新点 $theta_{t+1} = theta_t – alpha nabla J(theta_t)$，其中 $alpha$ 为学习率。
重复步骤 2 和 3，直到满足收敛条件。

2. 梯度下降法的变种

2.1 批量梯度下降法（BGD）

批量梯度下降法使用整个训练数据集来计算梯度，因此每次迭代的计算开销较大，但其优点是每次更新方向较为准确。适用于数据集较小的情况。

2.2 随机梯度下降法（SGD）

随机梯度下降法每次仅使用一个样本来计算梯度，因此计算速度较快，适合大规模数据集。其缺点是收敛过程中可能会出现较大波动。

2.3 小批量梯度下降法（MBGD）

小批量梯度下降法结合了批量和随机梯度下降法的优点，同时使用多个样本来计算梯度，既提高了计算效率，又减少了波动。

3. 梯度下降法的优缺点

3.1 优点

简单易实现，适用于多种问题。
能够处理大规模数据集。
适用于非凸优化问题。

3.2 缺点

可能陷入局部最优解。
需要调整学习率，学习率过大或过小都会影响收敛速度。
对初始值敏感，选择不当可能导致收敛困难。

4. 梯度下降法在机器学习中的应用

梯度下降法在机器学习中有广泛的应用，包括线性回归、逻辑回归和神经网络的训练。

4.1 在线性回归中的应用

线性回归模型通过最小化损失函数来拟合数据。梯度下降法通过调整模型参数，使得损失函数达到最小值，从而找到最佳拟合。

import numpy as np

X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])
y = np.dot(X, np.array([1, 2])) + 3

theta = np.zeros(2)
learning_rate = 0.01

for _ in range(1000):
    gradient = X.T.dot(X.dot(theta) - y) / len(y)
    theta -= learning_rate * gradient

print(f"Optimal parameters: {theta}")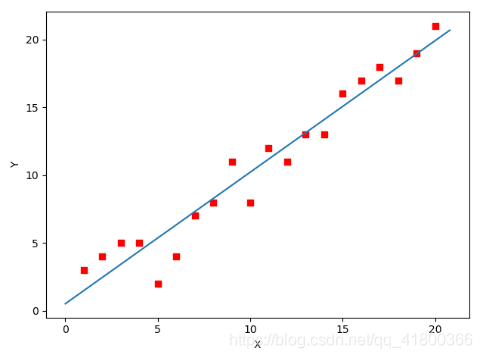

4.2 在逻辑回归中的应用

逻辑回归用于二分类问题，通过最大化似然函数来估计模型参数。梯度下降法通过最小化负对数似然函数实现参数估计。

4.3 在神经网络中的应用

神经网络通过反向传播算法进行训练，梯度下降法用于更新网络中的权重和偏置。

5. 梯度下降法的调优

调优是提高梯度下降法性能的重要步骤，主要包括学习率的选择和特征归一化。

5.1 学习率的选择

学习率决定了每次迭代的步伐，过大可能导致震荡，过小则收敛缓慢。常用的方法是使用自适应学习率算法，如AdaGrad、RMSProp等。

5.2 特征归一化

特征归一化可以加快收敛速度，常用的方法有标准化和归一化。

6. 代码实现

以下是一个使用Python实现梯度下降法的示例代码。

import numpy as np

theta = np.array([0.0, 0.0])
learning_rate = 0.01

X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])
y = np.dot(X, np.array([1, 2])) + 3

for _ in range(1000):
    gradient = np.dot(X.T, np.dot(X, theta) - y) / len(y)
    theta -= learning_rate * gradient

print(f"Optimal parameters: {theta}")

7. 结论

梯度下降法是机器学习中一个重要的优化工具，通过不断迭代优化模型参数，可以有效降低损失函数值，提高模型的预测能力。尽管存在一些缺点，如需调整学习率和可能陷入局部最优解，但通过合理的调优和改进，梯度下降法仍然是一个强大而灵活的优化方法。

FAQ

问：梯度下降法可以用于所有的优化问题吗？
- 答：梯度下降法主要用于连续可微函数的优化问题，对于离散或不可微函数问题，可能需要其他优化方法。
问：如何选择合适的学习率？
- 答：学习率可以通过实验选择，或者使用自适应学习率算法如AdaGrad、RMSProp等来自动调整。
问：梯度下降法如何避免陷入局部最优解？
- 答：可以通过多次随机初始化或使用动量法等技巧来增加探索全局最优解的机会。