探索拉格朗日点：太空中的平衡点

拉格朗日点是天体力学中一个迷人的概念，涉及到两个巨大天体之间的引力和一个小质量物体的离心力之间的平衡。本文将深入探讨拉格朗日点的构成、应用及其在现代航天中的重要性。

拉格朗日点的定义与历史

拉格朗日点，又称平动点，是指在两个大型天体的引力场中，存在五个特殊的点，这些点上一个小质量的物体可以保持相对静止。这一概念最早由数学家约瑟夫·路易·拉格朗日在1772年提出。

拉格朗日点的数学基础

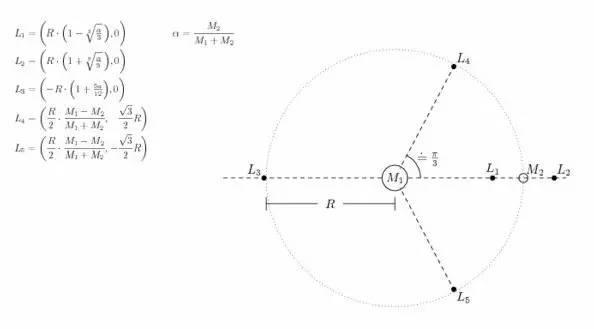
在天体力学中，拉格朗日点是限制性三体问题的五个特解。欧拉和拉格朗日通过研究二体系统的引力场推算出了这些点的位置：L1、L2、L3由欧拉推算出，而L4和L5则是由拉格朗日推算的。

代码块描述：拉格朗日点的计算公式

以下是计算拉格朗日点位置的伪代码示例：

import math

def calculate_lagrange_points(m1, m2, distance):
    # m1和m2为两个天体的质量，distance为两者之间的距离
    L1 = distance * (1 - (m2 / (3 * m1))**(1/3))
    L2 = distance * (1 + (m2 / (3 * m1))**(1/3))
    L3 = distance * (1 + 5 * (m2 / (12 * m1)))
    return L1, L2, L3

拉格朗日点的构成与位置

在行星和恒星系统中，常见的拉格朗日点有五个：L1、L2、L3、L4和L5。L1、L2和L3位于两大天体的连线上，而L4和L5则位于公转轨道的60度位置。

L1、L2、L3：不稳定的引力平衡点

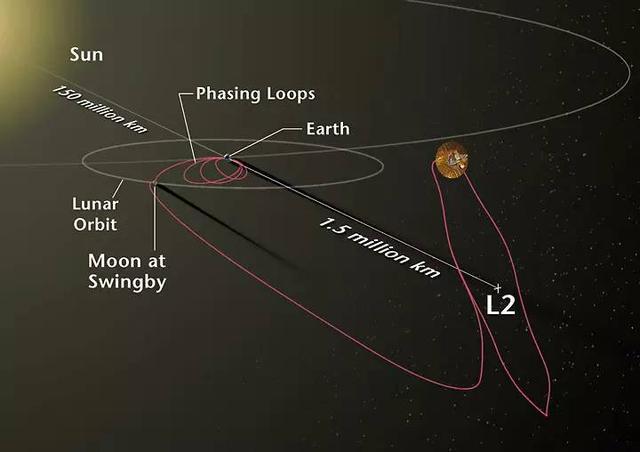
L1位于两大天体之间，是进行太阳观测的理想位置，如SOHO和深空气象卫星就位于此。L2则位于背向太阳的地球方向，适合深空观测，詹姆斯·韦伯太空望远镜将被部署在此进行宇宙红外辐射观测。L3虽然在科幻小说中常被提及，但在现实中尚未被实际利用。

稳定的L4和L5点

L4和L5在公转轨道上的60度位置上形成等边三角形，因其稳定性，被认为是可能的太空殖民区域。木星的特洛伊小行星群也聚集在L4和L5周围。

拉格朗日点的应用

太空观测与科学研究

拉格朗日点为科学研究提供了稳定的观测平台。L1和L2点特别适合安装天文望远镜和探测器，如SOHO和WMAP。

太空任务与探测器的部署

由于拉格朗日点的独特位置，许多太空任务选择这些点作为探测器的驻留位置。詹姆斯·韦伯太空望远镜将利用L2点来减少地球和太阳的光干扰，从而更有效地进行深空探测。

拉格朗日点在未来太空探索中的潜力

太空殖民的可能性

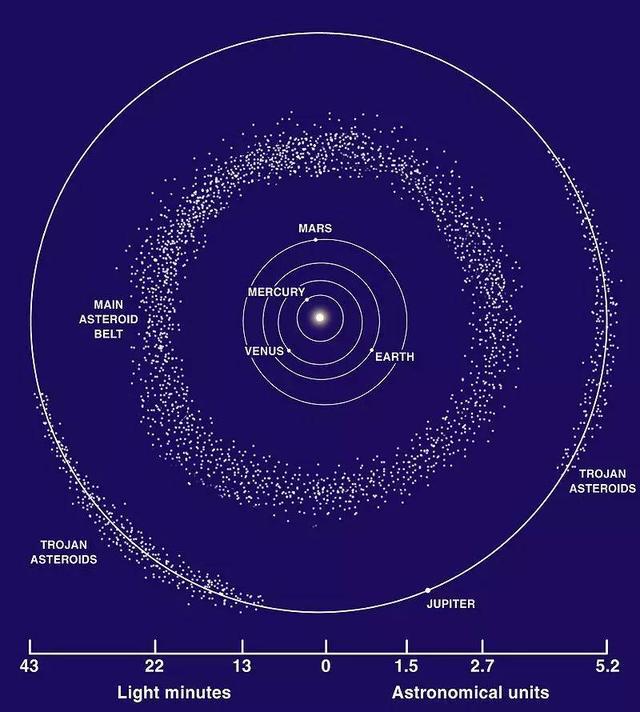
拉格朗日点提供了一个稳定的环境，适合未来太空殖民的研究。L4和L5因其稳定性，被认为是可能的太空殖民地。

技术挑战与解决方案

在这些点上，技术挑战包括保持轨道稳定性和进行有效的通讯。使用微调和轨道修正技术可以帮助解决这些问题。

结论

拉格朗日点为现代天文学和航天任务提供了无可比拟的优势。无论是在观测太阳系外的深空，还是作为未来太空殖民的前哨基地，拉格朗日点都具有巨大的潜力。

常见问题解答（FAQ）

1. 问：什么是拉格朗日点？

   • 答：拉格朗日点是指在两个天体的引力作用下，第三个小质量物体可以保持相对静止的点。

2. 问：L2点的主要用途是什么？

   • 答：L2点主要用于深空观测，能够提供稳定的环境，减少地球和太阳的干扰。

3. 问：为什么L4和L5点被认为是太空殖民的潜在地点？

   • 答：由于L4和L5点的稳定性，它们能自然积累物质，适合作为未来太空殖民的前哨基地。

4. 问：在拉格朗日点上部署探测器有哪些挑战？

   • 答：主要的挑战包括保持轨道稳定性和进行有效的通讯。

5. 问：L3点在现实中有应用吗？

   • 答：目前L3点尚未在现实中得到应用，主要存在于科幻小说中。