探索拉格朗日乘数法：从基础到应用

拉格朗日乘数法是一种在数学优化问题中用于寻找条件极值的方法。它通过引入拉格朗日乘子，将原本受限的问题转化为无约束优化问题，从而简化求解过程。这种方法广泛应用于多元函数的极值问题，特别是在经济学和工程学中具有重要意义。

在拉格朗日乘数法中，关键术语包括“拉格朗日乘子”、“约束条件”和“目标函数”。目标函数是需要优化的函数，约束条件是变量必须满足的限制条件，而拉格朗日乘子则是用于调整目标函数与约束之间关系的参数。

在数学中，偏导数和梯度是求解优化问题的基础工具。偏导数表示函数在某一方向上的变化率，而梯度则是所有偏导数的向量，指向函数增长最快的方向。在拉格朗日乘数法中，梯度用于判断目标函数与约束条件的相切性。

极值问题涉及找到函数的最大值或最小值。在有约束的情况中，函数的极值点不仅要满足目标函数的导数为零，还需满足约束条件。这时，拉格朗日乘数法通过构造一个新的函数，结合目标函数和约束条件，来寻找这些极值点。

考虑麻省理工学院数学课程中的一个经典问题：在双曲线 $xy=3$ 上找到离原点最近的点。通过拉格朗日乘数法，我们可以将这个问题转化为一个无约束的优化问题，从而简化求解过程。具体步骤包括构建拉格朗日函数，求解偏导数方程组，最终得到最优解。

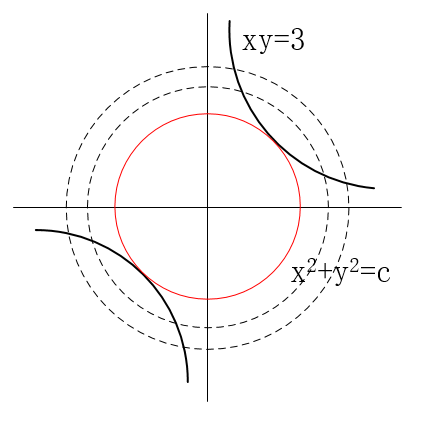
双曲线示意图

在更复杂的优化问题中，拉格朗日乘数法仍然表现出色。无论是经济学中的资源分配问题，还是工程学中的结构优化问题，拉格朗日乘数法都能通过引入多个乘子，灵活处理多约束条件的极值问题。

KKT条件，即Karush-Kuhn-Tucker条件，是拉格朗日乘数法的扩展，用于处理包含不等式约束的优化问题。KKT条件是非线性规划问题最优解的必要条件，它在现代优化理论中占据核心地位。

在KKT条件下，优化问题的解决不仅包括传统的等式约束，还涉及不等式约束的处理。KKT条件通过引入对偶变量，将不等式约束转化为等式约束，进而求解优化问题。

线性规划是优化问题的一种特殊形式，通常通过消元法和单纯形法求解。在此过程中，拉格朗日乘数法则提供了一种理论支持，用于解释约束条件和最优解之间的关系。

在凸优化问题中，拉格朗日乘数法同样适用。凸优化的特点是局部最优即为全局最优，这使得拉格朗日乘数法在求解过程中更加高效。通过将目标函数和约束条件构造成凸函数，优化问题得以简化。

在实际应用中，拉格朗日乘数法可能面临约束条件复杂、解不唯一等问题。为了应对这些挑战，通常需要结合数值模拟和计算机辅助设计等方法，以提高解的精度和效率。

为了解决复杂约束问题，可以采用迭代优化、逐步放松约束条件等策略。同时，利用现代计算机技术，可以快速处理大规模数据，进一步提升拉格朗日乘数法的应用效果。

随着科学技术的进步，拉格朗日乘数法在新兴领域的应用前景广阔。例如，在机器学习中的参数优化、图像处理中的边缘检测等方面，拉格朗日乘数法都有可能发挥重要作用。

未来，随着算法的不断改进和计算能力的提升，拉格朗日乘数法将在更广泛的领域内得到应用。尤其是在处理高维数据和多目标优化问题时，该方法的优势将更加凸显。

问：拉格朗日乘数法主要解决什么类型的问题？
- 答：拉格朗日乘数法主要用于解决多变量函数的极值问题，特别是在存在约束条件的情况下，如等式和不等式约束。
问：如何判断一个问题是否适合使用拉格朗日乘数法？
- 答：如果问题涉及求解在特定约束下的最优值，并且约束条件可以转换为等式或不等式形式，那么拉格朗日乘数法可能是一个合适的选择。
问：拉格朗日乘数法与KKT条件有什么关系？
- 答：KKT条件是拉格朗日乘数法的扩展，适用于包含不等式约束的优化问题。KKT条件为求解此类问题提供了必要条件，且在凸优化中为充要条件。