行列式展开：理论与应用

行列式在数学和工程学中扮演着至关重要的角色，它不仅是矩阵运算的核心工具之一，也是理解线性代数的基础。在这篇文章中，我们将深入探讨行列式展开的各种定理和性质，并通过具体示例和图解加深理解。

1. 行列式按行（列）展开定理

行列式按行（列）展开定理是行列式计算的基本方法之一。它基于对矩阵的某一行（或列）的元素进行展开，将行列式简化为更小阶的行列式之和。

1.1 余子式的概念

余子式是指从行列式中去除某个元素所在的行和列后剩下的行列式。假设我们有一个行列式 $D$：

$$D = begin{vmatrix} 1 & 1 & 0
1 & 1 & 1
2 & 3 & 4
end{vmatrix}$$

其余子式 $M_{32}$ 就是去掉第三行和第二列后得到的行列式：

$$M_{32} = begin{vmatrix} 1 & 0
1 & 1
end{vmatrix}$$

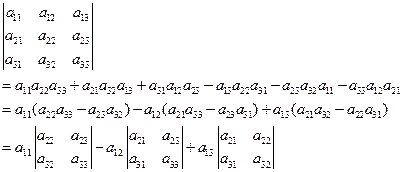
余子式示例

1.2 代数余子式

代数余子式是在余子式前加上 $(-1)^{i+j}$ 的符号，其中 $i$ 和 $j$ 分别表示元素的行号和列号。这样处理是为了保持行列式展开的符号一致性。

1.3 按行（列）展开定理

行列式的值等于其任意一行（列）各元素与其代数余子式乘积之和。按行展开公式为：

$$D = a{i1}A{i1} + a{i2}A{i2} + … + a{in}A{in}$$

按列展开公式类似，适用于列的元素。选择包含较多零元素的行（列）进行展开可以简化计算。

2. 异乘变零定理

异乘变零定理指出，若行列式中某行（列）元素与另一行（列）元素的代数余子式相乘后累加，其和为零。这一性质在简化计算中非常有用。

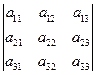
异乘变零示例

2.1 理论解释

假设行列式 $D$：

$$D = begin{vmatrix} 1 & 1 & 2 & 3
0 & 0 & 8 & 9
2 & 2 & 5 & 4
9 & 9 & 9 & 10
end{vmatrix}$$

用第4行元素与第1行元素的代数余子式相乘：

$$9A{11} + 9A{12} + 9A{13} + 10A{14} = 0$$

2.2 应用

通过构造新的行列式验证异乘变零定理，可以帮助我们寻找行列式的解或简化复杂的运算过程。

3. 拉普拉斯定理

拉普拉斯定理允许我们将行列式展开为多个小阶的行列式，是理解高阶行列式计算的关键工具。

3.1 k阶子式

k阶子式是指从n阶行列式中取定k行和k列，所形成的交叉元素构成的行列式。通过去掉这些行和列，我们得到余子式。

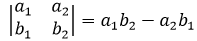
k阶子式示例

3.2 拉普拉斯展开

在n阶行列式中，任意选定k行，由这些行元素组成的k阶子式与对应的代数余子式乘积之和等于行列式的值。

4. 行列式相乘定理

当两个同阶行列式相乘时，其结果为一个新的行列式。行列式相乘定理为我们提供了一个计算复杂矩阵乘积的新方法。

4.1 运算规则

假设行列式 $D_1$ 和 $D_2$，相乘后的第1行第1个元素为 $D_1$ 的第1行与 $D_2$ 的第1列元素相乘之和，以此类推。

4.2 示例

$$begin{vmatrix} 1 & 1 & 1
2 & 0 & 0
0 & 0 & 3
end{vmatrix} times begin{vmatrix} 1 & 2 & 3
1 & 3 & 2
3 & 2 & 1
end{vmatrix} = begin{vmatrix} 5 & 7 & 6
2 & 4 & 6
9 & 6 & 3
end{vmatrix}$$

5. 行列式的性质

行列式的性质帮助我们理解其几何意义和代数特性。

5.1 性质0：单位矩阵的行列式为1

单位矩阵是行列式为1的特殊矩阵。

5.2 性质1：全零行导致行列式为0

如果行列式中某行或某列元素全为0，则行列式的值为0。

5.3 性质2：成比例行导致行列式为0

如果两行（列）成比例，则行列式为0。

6. 行列式的意义

行列式不仅是一个数值，更是向量间关系的刻画。行列式不为零说明向量独立，反之则不独立。

6.1 几何意义

行列式在几何上表示向量围成图形的面积或体积。例如，二维平面中由两个向量围成的平行四边形的面积就是行列式的值。

6.2 方程组解的判别

行列式的值影响方程组的解。当行列式不为零时，方程组有唯一解；为零时，可能无解或有无数解。

7. 行列式计算技巧

利用行列式的性质和定理，我们可以简化计算。

7.1 消元法

通过消元法将矩阵转换为上三角矩阵，行列式的值等于主对角线元素的乘积。

7.2 行列式公式

行列式的公式可以用于计算复杂矩阵的行列式值。对于n阶矩阵，行列式的计算复杂度通常较高，但公式提供了一种系统化的计算方法。

FAQ

问：行列式展开的实用意义是什么？
- 答：行列式展开使得高阶行列式的计算变得可行，并且是线性代数中许多其他定理和应用的基础。
问：如何选择展开的行或列？
- 答：通常选择包含最多零元素的行或列进行展开，以简化计算过程。
问：行列式值为零意味着什么？
- 答：行列式值为零意味着矩阵行或列之间存在线性相关性，导致解的独立性丧失。
问：行列式如何应用于方程组求解？
- 答：通过行列式可以判断方程组的解是否唯一，并通过克拉默法则求解。
问：行列式的几何解释是什么？
- 答：行列式在几何上表示由向量围成图形的面积或体积，反映了向量的独立性。