函数图像与其应用详解
函数图像在数学中扮演着重要角色，不仅帮助我们直观地理解函数性质，还为我们解决实际问题提供了工具。在这篇文章中，我们将深入探讨各种函数图像的特性及其应用，包括初等函数、三角函数、反三角函数及其相关公式。同时，我们将结合具体的代码示例和图片链接，帮助您更好地理解这些概念。最后，我们还将解答一些常见问题，帮助您巩固所学知识。
初等函数图像
常数函数的图像
常数函数的形式为 $y = C$，其中 $C$ 为常数。不论输入变量如何变化，其输出值始终为固定的常数。其图像是一条水平直线，平行于 $x$ 轴。常数函数在数学分析中用于描述恒定不变的数量。
一次函数的图像
一次函数，或称线性函数，具有形式 $y = mx + b$。其图像是一条直线，其中 $m$ 是斜率，决定了直线的倾斜程度，而 $b$ 是截距，表示直线在 $y$ 轴上的交点。一次函数广泛用于描述线性关系。
反比例函数的图像
反比例函数的形式为 $y = frac{1}{x}$。其图像是一条双曲线，分布在第一和第三象限，随着 $x$ 的绝对值增大，函数值逐渐接近于零。反比例函数常用于描述反向相关的关系。
二次函数的图像
二次函数以 $y = ax^2 + bx + c$ 表示，其图像是一条抛物线。参数 $a$ 决定了抛物线的开口方向和宽窄，$b$ 和 $c$ 影响其顶点的位置。二次函数在物理学中用于描述抛物运动。
指数函数的图像
指数函数具有形式 $y = a^x$，其中 $a$ 是底数。其图像随 $x$ 增大呈指数增长，当 $0 < a < 1$ 时，函数是递减的。当 $a > 1$ 时，函数是递增的。指数函数广泛应用于金融和人口增长模型中。
三角函数图像
正弦函数图像
正弦函数 $ ext{sin}(x)$ 是周期函数，其图像是一条波动的曲线，周期为 $2pi$。正弦函数常用于描述周期性现象，如声波和光波。
余弦函数图像
余弦函数 $ ext{cos}(x)$ 也是周期函数，与正弦函数相似，但其相位不同，周期同样为 $2pi$。余弦函数用于描述振动和波动现象。
正切函数图像
正切函数 $ ext{tan}(x)$ 的周期为 $pi$，其图像在每个周期内有不连续的竖直渐近线。正切函数用于表示角度的比率。
反三角函数图像
反正弦函数图像
反正弦函数 $ ext{arcsin}(x)$ 是正弦函数的反函数，其定义域为 $[-1, 1]$，值域为 $[-frac{pi}{2}, frac{pi}{2}]$。反正弦函数用于计算给定正弦值对应的角度。
反余弦函数图像
反余弦函数 $ ext{arccos}(x)$ 对应余弦函数，其定义域为 $[-1, 1]$，值域为 $[0, pi]$。反余弦函数用于计算给定余弦值对应的角度。
反正切函数图像
反正切函数 $ ext{arctan}(x)$ 是正切函数的反函数，其图像在 $(-infty, infty)$ 上连续。反正切函数用于计算给定正切值对应的角度。
三角函数公式
两角和与差公式
三角函数的两角和与差公式帮助我们将多个角度的函数简化为更易处理的形式。例如：
- $ ext{sin}(A + B) = ext{sin}A ext{cos}B + ext{cos}A ext{sin}B$
- $ ext{cos}(A + B) = ext{cos}A ext{cos}B – ext{sin}A ext{sin}B$
这些公式广泛应用于物理和工程计算中，尤其是在波动和信号处理领域。
倍角公式
倍角公式用于将角度的倍数函数表示为单个角度的函数，如：
- $ ext{tan}(2A) = frac{2 ext{tan}A}{1 – ext{tan}^2A}$
倍角公式在多角度问题中非常有用，如计算光的干涉和衍射。
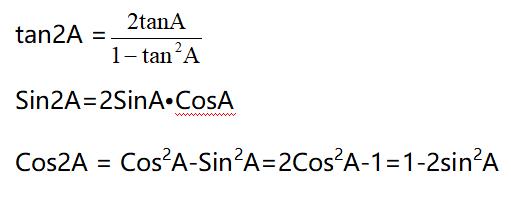
半角公式
半角公式用于将半角的三角函数表示为单角的函数：
- $ ext{sin}(frac{A}{2}) = sqrt{frac{1 – ext{cos}A}{2}}$
这些公式在计算精度要求高的场合非常重要，如数值分析。
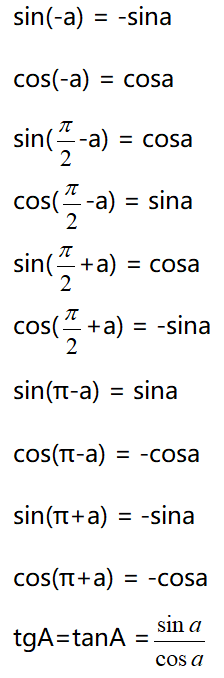
常见问题解答（FAQ）
-
问：函数图像如何帮助我们理解函数的性质？
- 答：函数图像通过视觉化的方式展示函数的变化趋势和关键特性，如对称性、周期性和渐近行为，帮助我们更直观地分析和理解函数的性质。
-
问：如何使用三角函数公式解决实际问题？
- 答：三角函数公式可以用于简化复杂的角度计算，如在物理学中的波动分析和工程中的信号处理，通过这些公式，可以将复杂计算转化为更易解决的形式。
-
问：反三角函数在计算中有哪些应用？
- 答：反三角函数主要用于求解给定三角函数值对应的角度，广泛应用于导航、测量和信号处理等领域。
通过本文的详细讲解，我们希望您能更好地理解函数图像及其相关的三角函数公式，并能够应用于实际问题的解决中。
