最小生成树算法详解及应用

1. 最小生成树概念

在图论中，最小生成树（Minimum Spanning Tree, MST）是一个连通无向图的子图，其中包括所有的顶点，并且边的总权重最小。最小生成树在许多实际应用中都有广泛的应用，如网络设计、城市道路规划等。只有连通图才有生成树，而对于非连通图，只存在生成森林。

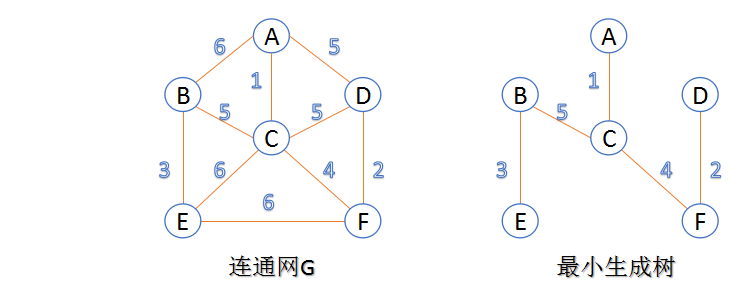
最小生成树示意图

1.1 连通图与生成树

一个连通图是指在无向图中，任意两个顶点之间都有路径相通。生成树则是该连通图的一个极小连通子图，包含所有顶点且无环路。最小生成树是指生成树中所有边的权重之和最小的那一棵。

1.2 生成树的性质

一个连通图可以有多个生成树，每个生成树包含相同的顶点个数和边数。生成树中没有环，但移除任何一条边会导致图不连通。对于包含 n 个顶点的连通图，生成树包含 n 个顶点和 n-1 条边。

2. Kruskal算法详解

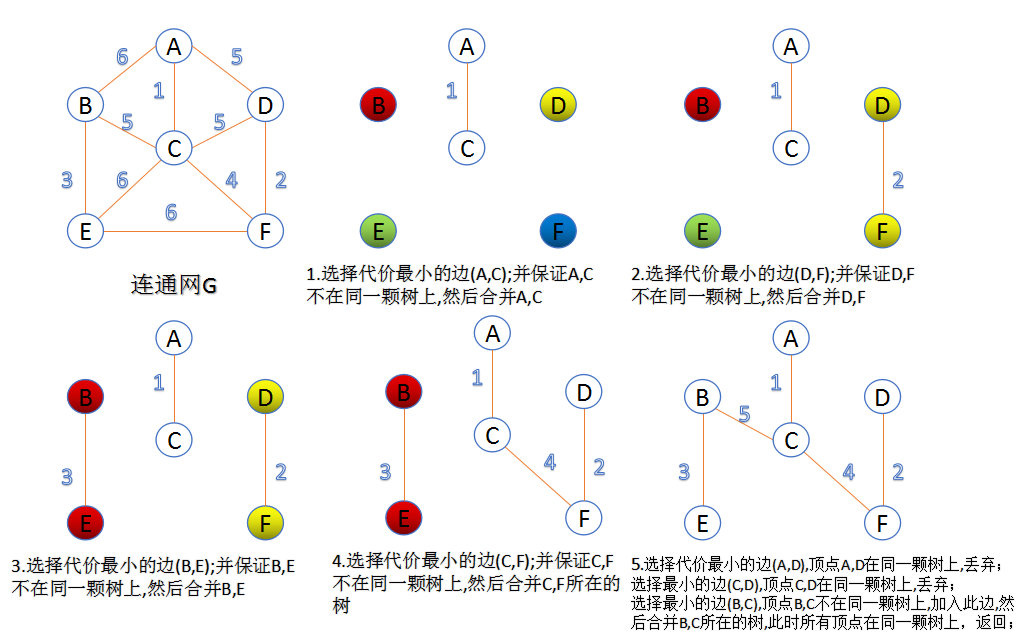
Kruskal算法是最小生成树的一种经典算法，其基本思想是将所有边按权重从小到大排序，然后依次选择权重最小且不形成环的边加入生成树，直到生成树包含 n-1 条边。

Kruskal算法示意图

2.1 Kruskal算法步骤

将图中的所有边按权重从小到大排序。
初始化 n 个顶点为 n 棵独立的树组成的森林。
依次选择权重最小的边，如果边的两个顶点属于不同的树，则将这两个树合并。
重复第3步，直到所有顶点都在同一颗树内，或者有 n-1 条边。

2.2 Kruskal算法的实现

#include 
#include 
#include 
using namespace std;

struct Edge {
    int u, v, weight;
    bool operator<(const Edge& e) const {
        return weight < e.weight;
    }
};

int findParent(int v, vector& parent) {
    if (parent[v] != v)
        parent[v] = findParent(parent[v], parent);
    return parent[v];
}

void kruskal(int vertexCount, vector& edges) {
    sort(edges.begin(), edges.end());
    vector parent(vertexCount);
    vector mst;
    for (int i = 0; i < vertexCount; ++i)
        parent[i] = i;

    for (const Edge& edge : edges) {
        int uParent = findParent(edge.u, parent);
        int vParent = findParent(edge.v, parent);
        if (uParent != vParent) {
            mst.push_back(edge);
            parent[uParent] = vParent;
        }
    }

    for (const Edge& edge : mst)
        cout << edge.u << " - " << edge.v << " : " << edge.weight << endl;
}

3. Prim算法详解

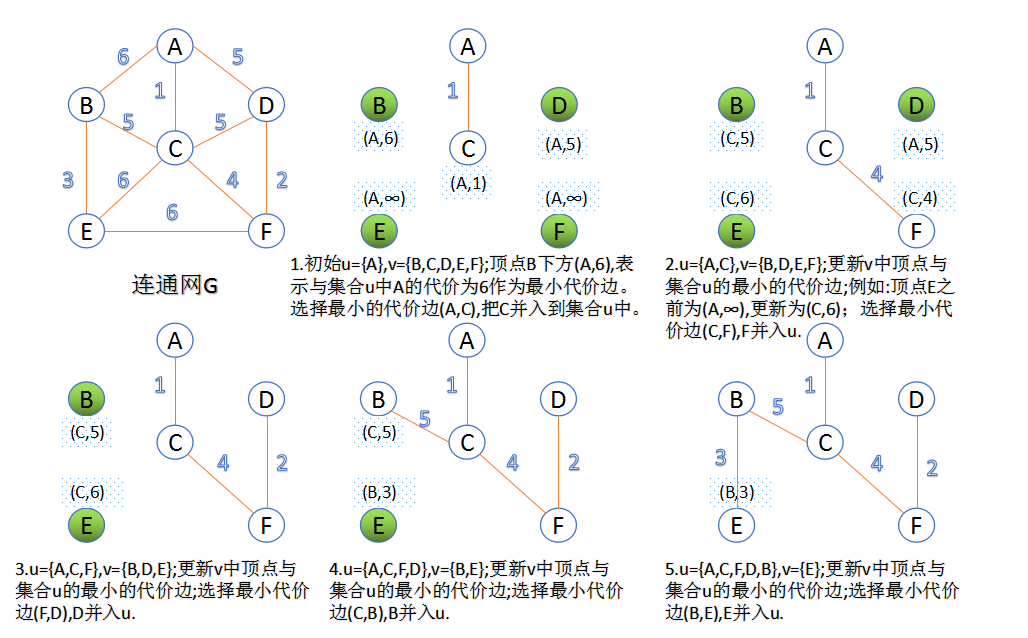
Prim算法是另一种求最小生成树的方法，与Kruskal算法不同，Prim算法是从一个顶点开始，逐渐扩展生成树，直到覆盖所有顶点。

Prim算法示意图

3.1 Prim算法步骤

从任意一个顶点开始，加入生成树。
在生成树和集合中，选择一条代价最小的边，将相关顶点加入生成树。
重复第2步，直到生成树包含 n 个顶点。

3.2 Prim算法的实现

#include 
#include 
#include 
using namespace std;

#define V 5

int minKey(int key[], bool mstSet[])
{
    int min = INT_MAX, min_index;

    for (int v = 0; v < V; v++)
        if (mstSet[v] == false && key[v] < min)
            min = key[v], min_index = v;

    return min_index;
}

void primMST(int graph[V][V])
{
    int parent[V];
    int key[V];
    bool mstSet[V];

    for (int i = 0; i < V; i++)
        key[i] = INT_MAX, mstSet[i] = false;

    key[0] = 0;
    parent[0] = -1;

    for (int count = 0; count < V - 1; count++) {
        int u = minKey(key, mstSet);

        mstSet[u] = true;

        for (int v = 0; v < V; v++)
            if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v])
                parent[v] = u, key[v] = graph[u][v];
    }

    for (int i = 1; i < V; i++)
        cout << parent[i] << " - " << i << " n";
}

4. Kruskal与Prim的比较

虽然Kruskal和Prim算法都可以用于求解最小生成树，但它们适用于不同类型的图。Kruskal算法适用于稀疏图，因为它处理的是边的集合，而Prim算法适用于稠密图，因为它处理的是顶点的集合。

4.1 适用场景

Kruskal更适合边数较少的图（稀疏图）。
Prim更适合边数较多的图（稠密图）。

4.2 算法复杂度

Kruskal算法主要依赖于对边的排序，复杂度为O(E log E)。
Prim算法的复杂度为O(V^2)或O(E log V)（使用优先队列优化）。

5. 最小生成树的应用

最小生成树在许多实际问题中都有应用。例如，通信网络设计中，我们希望连接所有节点并且总成本最小，或者在城市规划中，我们希望修建最少的道路连接所有区域。

5.1 网络设计

在网络设计中，最小生成树可以用于确定最优的连接路径，以降低网络成本并提高效率。通过选择最小的权重边，我们可以确保网络的总成本达到最小。

5.2 城市规划

在城市规划中，最小生成树可以帮助确定要修建的道路或管道的最小集合，使所有城市都能互相连通，从而节省建设成本。

6. 代码实现与优化

在实际开发中，最小生成树算法可以使用多种编程语言实现。以下是一些常见的实现语言和优化方法。

6.1 C++实现

C++是一种高效的系统级编程语言，可以用于实现复杂的算法，如最小生成树的Kruskal和Prim算法。

6.2 Python实现

Python因其简洁和可读性强而被广泛使用。尽管Python在性能上不如C++，但它提供了丰富的库和工具来实现图算法。

7. 总结与展望

最小生成树算法是图论中的经典问题，具有重要的理论意义和实际应用价值。通过学习Kruskal和Prim算法，我们可以更好地解决实际问题中的最小生成树问题。在未来，随着计算机性能的提升和算法的优化，最小生成树算法将会得到更广泛的应用。

FAQ

1. 什么是最小生成树？

最小生成树是指在一个连通无向图中，包含所有顶点且边的权重之和最小的生成树。

2. Kruskal算法和Prim算法有什么区别？

Kruskal算法是基于边的选择，适用于稀疏图；而Prim算法是基于顶点的选择，适用于稠密图。

3. 为什么要使用最小生成树算法？

最小生成树算法可以帮助找到连接所有节点的最优路径，从而降低网络成本或建设成本，广泛应用于网络设计和城市规划等领域。

4. 如何选择使用Kruskal还是Prim算法？

选择算法时需根据图的稀疏程度：对于稀疏图，选择Kruskal算法；对于稠密图，选择Prim算法。

5. 最小生成树算法有哪些优化方法？

最小生成树算法可以通过数据结构的优化（如使用并查集或优先队列）来提高效率，适用于大规模图的处理。