深入了解DQN网络：原理与实现

DQN（Deep Q-Network）是一种结合深度学习和强化学习的革命性算法，已在许多复杂的任务中展现出卓越的性能。本文将深入探讨DQN网络的原理、实现及其在实际应用中的表现，并提供相关代码示例和FAQ解答。

DQN网络的核心思想

DQN网络的核心在于将深度学习与强化学习相结合，突破了传统Q-learning在高维状态空间中的局限性。传统Q-learning使用Q表来存储每个状态-动作对的Q值，但当状态和动作空间过于庞大时，Q表的存储和计算成本变得不可承受。DQN通过神经网络来逼近Q值函数，从而解决了这一问题。

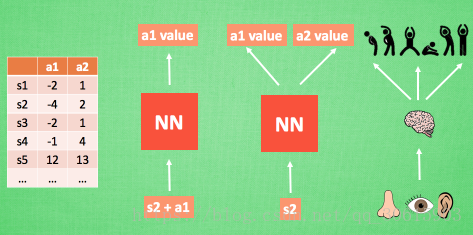
DQN网络示意图

在DQN中，深度神经网络用于学习状态特征，进而预测每个可能动作的Q值。这使得DQN能够在复杂的高维状态空间中高效运作，特别是在游戏和机器人控制等领域表现出色。

经验回放机制

DQN中的经验回放机制通过存储智能体与环境的交互过程，打破了样本之间的时间相关性。经验回放库中存储了大量的历史经验，训练时从中随机抽取样本，这样的随机化处理打破了样本之间的相关性，有助于提高训练的稳定性和效率。

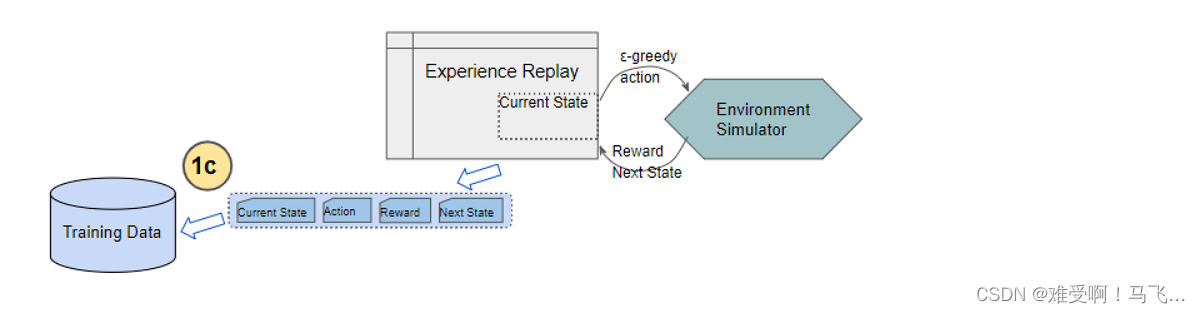
经验回放示意图

经验回放的另一个好处是能够重复利用经验，充分挖掘已有数据的价值。这种机制在资源有限的情况下尤为重要。

目标网络的作用

DQN使用两个神经网络：在线网络和目标网络。在线网络用于选择动作，而目标网络用于计算目标Q值。目标网络的参数并不会立即更新，而是在一定步数后与在线网络同步。这种设计减少了目标Q值的波动，增强了训练的稳定性。

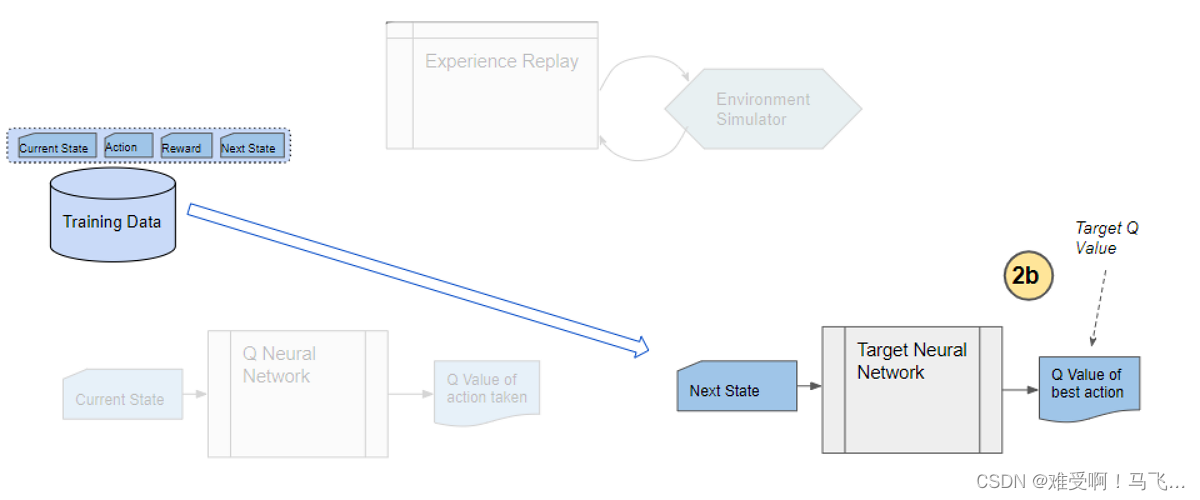
目标网络示意图

目标网络的稳定性使得DQN在训练过程中能够逐渐逼近最优策略，而不是在不稳定的目标值上反复震荡。

DQN的训练过程

DQN的训练过程包括以下几个步骤：

初始化：初始化在线网络和目标网络，并创建经验回放缓冲区。
选择动作：使用ε-greedy策略选择动作，确保在探索和利用之间保持平衡。
存储经验：将当前状态、动作、奖励和下一个状态存储到经验回放缓冲区中。
更新网络：从经验回放缓冲区中随机抽取样本，计算目标Q值和预测Q值之间的误差，并通过反向传播更新在线网络的参数。
同步网络：每隔一定步数，将在线网络的参数复制到目标网络。

这种训练过程的设计使得DQN能够充分利用历史经验，稳定地逼近最优策略。

DQN在游戏中的应用

DQN在Atari 2600游戏中的表现令人瞩目。通过学习像素级别的游戏画面，DQN能够在多个游戏中达到甚至超越人类玩家的水平。DQN的成功展示了深度强化学习在处理复杂视觉输入和策略规划中的潜力。

Atari游戏示意图

这种能力的实现得益于神经网络对复杂特征的提取和强化学习策略的优化，DQN能够在多样化的游戏场景中表现出色。

DQN的代码实现

以下是一个简单的DQN代码实现示例，使用Python和TensorFlow构建。

import numpy as np
import tensorflow as tf

class DeepQNetwork:
    def __init__(self, n_actions, n_features, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9, replace_target_iter=300, memory_size=500, batch_size=32, e_greedy_increment=None, output_graph=True):
        self.n_actions = n_actions
        self.n_features = n_features
        self.lr = learning_rate
        self.gamma = reward_decay
        self.epsilon_max = e_greedy
        self.replace_target_iter = replace_target_iter
        self.memory_size = memory_size
        self.batch_size = batch_size
        self.epsilon_increment = e_greedy_increment
        self.epsilon = 0 if e_greedy_increment is not None else self.epsilon_max
        self.learn_step_counter = 0
        self.memory = np.zeros((self.memory_size, n_features * 2 + 2))
        self._build_net()
        t_params = tf.get_collection('target_net_params')
        e_params = tf.get_collection('eval_net_params')
        self.replace_target_op = [tf.assign(t, e) for t, e in zip(t_params, e_params)]
        self.sess = tf.Session()
        if output_graph:
            tf.summary.FileWriter('logs/', self.sess.graph)
        self.sess.run(tf.global_variables_initializer())
        self.cost_his = []

    def _build_net(self):
        self.s = tf.placeholder(tf.float32, [None, self.n_features], name='s')
        self.q_target = tf.placeholder(tf.float32, [None, self.n_actions], name='Q_target')
        with tf.variable_scope('eval_net'):
            c_names, n_l1, w_initializer, b_initializer = ['eval_net_params', tf.GraphKeys.GLOBAL_VARIABLES], 10, tf.random_normal_initializer(0., 0.3), tf.constant_initializer(0.1)
            with tf.variable_scope('l1'):
                w1 = tf.get_variable('w1', [self.n_features, n_l1], initializer=w_initializer, collections=c_names)
                b1 = tf.get_variable('b1', [1, n_l1], initializer=b_initializer, collections=c_names)
                l1 = tf.nn.relu(tf.matmul(self.s, w1) + b1)
            with tf.variable_scope('l2'):
                w2 = tf.get_variable('w2', [n_l1, self.n_actions], initializer=w_initializer, collections=c_names)
                b2 = tf.get_variable('b2', [1, self.n_actions], initializer=b_initializer, collections=c_names)
                self.q_eval = tf.matmul(l1, w2) + b2
        with tf.variable_scope('loss'):
            self.loss = tf.reduce_mean(tf.squared_difference(self.q_target, self.q_eval))
        with tf.variable_scope('train'):
            self._train_op = tf.train.RMSPropOptimizer(self.lr).minimize(self.loss)
        self.s_ = tf.placeholder(tf.float32, [None, self.n_features], name='s_')
        with tf.variable_scope('target_net'):
            c_names = ['target_net_params', tf.GraphKeys.GLOBAL_VARIABLES]
            with tf.variable_scope('l1'):
                w1 = tf.get_variable('w1', [self.n_features, n_l1], initializer=w_initializer, collections=c_names)
                b1 = tf.get_variable('b1', [1, n_l1], initializer=b_initializer, collections=c_names)
                l1 = tf.nn.relu(tf.matmul(self.s_, w1) + b1)
            with tf.variable_scope('l2'):
                w2 = tf.get_variable('w2', [n_l1, self.n_actions], initializer=w_initializer, collections=c_names)
                b2 = tf.get_variable('b2', [1, self.n_actions], initializer=b_initializer, collections=c_names)
                self.q_next = tf.matmul(l1, w2) + b2

以上代码展示了如何构建一个简单的DQN网络，包括目标网络和在线网络的定义。神经网络的结构可以根据具体任务进行调整。

DQN的挑战与改进

尽管DQN在许多任务中表现出色，但仍然面临一些挑战，如样本效率低、长时间依赖性等。为此，研究人员提出了多种改进方法，如双DQN、优先经验回放、A3C等，以进一步提高DQN的性能和稳定性。

改进示意图

这些改进方法在不同的应用场景中展现出良好的效果，使得DQN及其变种在研究和工业界广泛应用。

FAQ

问：DQN与传统Q-learning的主要区别是什么？
- 答：DQN通过神经网络逼近Q值函数，解决了传统Q-learning在高维状态空间中的存储和计算问题。
问：DQN如何保证训练的稳定性？
- 答：DQN通过经验回放和目标网络机制减少样本相关性和目标值的波动，提高训练稳定性。
问：DQN能否应用于非视觉输入的任务？
- 答：可以，DQN可以处理各种形式的输入，只需根据任务需求调整神经网络结构。
问：如何选择DQN中的超参数？
- 答：超参数选择通常依赖于经验和实验，常用方法包括网格搜索和随机搜索。
问：DQN在实际应用中有哪些限制？
- 答：DQN在样本效率和长时间依赖性方面存在挑战，需结合其他方法进行改进。