函数与映射的深度解析

数学中的基本概念：函数与映射

函数与映射是数学中两个核心概念，它们在数学分析、代数以及其他领域中有着广泛的应用。理解这些概念不仅能提高数学学习的效率，还能为解决复杂的数学问题奠定基础。从广义上讲，函数是一种特殊的映射，而映射则是定义在两个集合之间的一种关系。

函数的定义与性质

函数是从一个集合到另一个集合的映射，这种映射具有单一性，即每个元素在一个集合中只能对应到另一个集合中的一个特定元素。函数通常用f(x)表示，其中x是自变量，f(x)是因变量。在数学中，函数的定义域是所有可能输入值的集合，而值域是所有可能输出值的集合。函数的特性包括：

1. 单一性：对于集合A中的每一个元素x，集合B中都有唯一的元素y与之对应。
2. 全定义性：函数的定义域必须在其定义中被完全指定。
3. 确定性：给定一个x，f(x)的值是确定的。

映射的定义与分类

映射是数学中两个集合之间的一种关系，这种关系规定了如何将一个集合中的元素对应到另一个集合中的元素。映射可以是单射、满射或双射，且不局限于数集与数集之间，也可以是不同类型的集合之间。

1. 单射（Injective）：每个元素在定义域中对应到不同的值域元素。
2. 满射（Surjective）：所有值域中的元素至少有一个定义域中的元素与之对应。
3. 双射（Bijective）：既是单射又是满射。

映射与函数的关系

函数可以视为一种特殊的映射，其定义域和值域都为数集。映射的广义性使得不仅限于数集之间，还可以是任何集合到另一个集合的关系。因此，所有的函数都是映射，但不是所有的映射都是函数。

映射的三种特性

映射具有三个基本特性：有序性、存在性和唯一性。这些特性确保了映射的方向性、每个元素的存在关系以及对应的唯一性。

有序性

映射是有方向的，从集合A到集合B的映射与从集合B到集合A的映射通常不同。

存在性

对于集合A中的任何一个元素，集合B中都存在一个元素与之对应。

唯一性

对于集合A中的任何一个元素，在集合B中和它对应的元素是唯一的。

逆映射与复合映射

逆映射是指一种映射关系的逆过程，即从值域返回到定义域的过程。复合映射是将两个或多个映射组合成一个新的映射。

逆映射的性质

逆映射存在的条件是原映射必须是双射，因为只有双射才具有可逆性。逆映射在数学分析中有重要的应用，尤其是在求解方程和逆变换中。

复合映射的应用

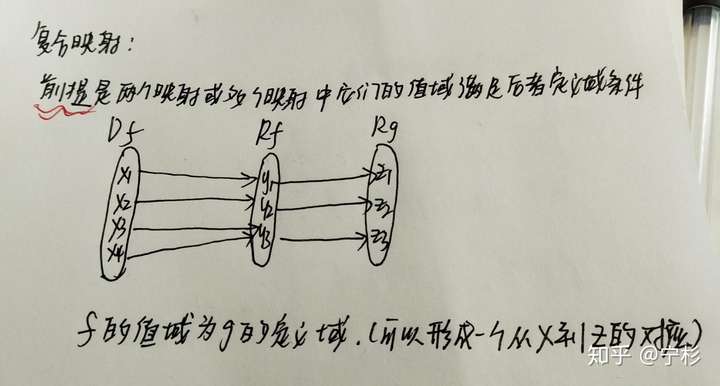
复合映射是多个映射的组合，可以简化复杂的映射关系。在函数复合中，如果g是从集合B到集合C的映射，f是从集合A到集合B的映射，则复合映射g∘f是从集合A到集合C的映射。

函数的应用

函数广泛应用于数学建模、物理学、经济学等领域，是描述自然现象和解决实际问题的有力工具。

函数的性质和类型

函数有多种类型，包括线性函数、二次函数、多项式函数、指数函数、对数函数等。理解函数的类型和性质可以帮助我们更好地分析问题。

1. 奇偶性：函数可以是奇函数、偶函数或既非奇也非偶。
2. 单调性：函数可以是单调递增或单调递减。
3. 周期性：一些函数具有周期性，如三角函数。

初等函数与复合函数

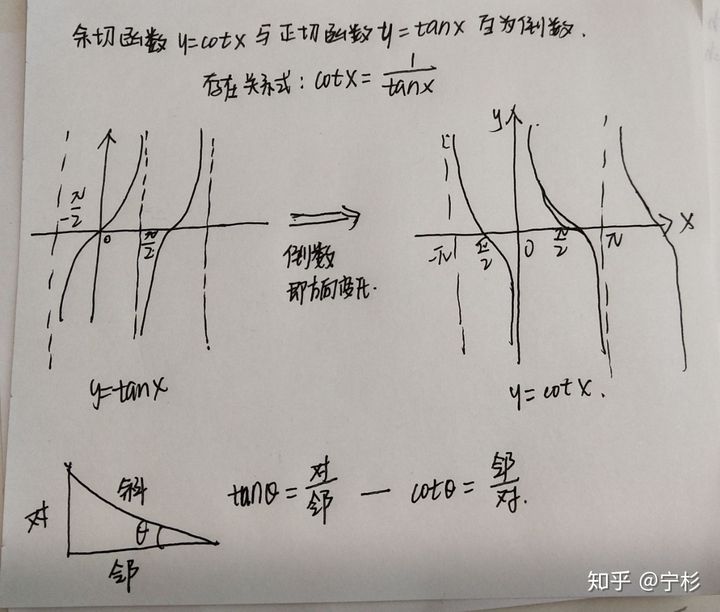
初等函数是通过有限次的四则运算和复合运算所构成的函数，包括多项式函数、指数函数、对数函数、三角函数等。复合函数是将多个函数组合成一个新的函数。

FAQ

问：函数与映射的区别是什么？

答：函数是定义在两个非空数集之间的特殊映射，而映射是定义在两个集合之间的关系，可以是数集之间或其他集合之间的关系。

问：什么是逆映射？

答：逆映射是一种映射关系的逆过程，即从值域返回到定义域的过程。只有在映射是双射时，逆映射才存在。

问：映射的三种特性是什么？

答：映射的三种特性是有序性、存在性和唯一性。这些特性确保了映射的方向性、每个元素的存在关系以及对应的唯一性。

问：如何判断两个函数是否相同？

答：判断两个函数是否相同可以通过比较它们的定义域和对应法则。如果两个函数的定义域和对应法则都相同，则这两个函数相同。

问：初等函数与复合函数有什么区别？

答：初等函数是通过有限次的四则运算和复合运算所构成的函数，如多项式函数、指数函数、三角函数等。复合函数是将多个函数组合成一个新的函数，用于描述更复杂的关系。