特征值与特征向量的深度解析

特征值和特征向量是线性代数中的核心概念，它们不仅在数学领域有着重要的地位，也在工程和科学计算中扮演着关键角色。本文将深入探讨特征值和特征向量的定义、计算方法以及实际应用，并通过实例演示如何求解特征值和特征向量。

特征值和特征向量的定义

特征值和特征向量是描述矩阵在线性变换中的缩放因子和方向的数学对象。对于一个给定的方阵oxed{A}，如果存在一个非零向量oxed{v}和一个标量oxed{ ext{λ}}，使得oxed{Av = λv}，则称oxed{ ext{λ}}为矩阵oxed{A}的特征值，oxed{v}为对应的特征向量。这个关系也常写作oxed{(A – λI)v = 0}，其中oxed{I}是单位矩阵。

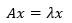
特征值和特征向量的关系

特征值的几何意义

特征值在几何上表示的是矩阵变换下的缩放比例。如果一个向量在矩阵变换下方向不变，那么这个向量就是特征向量，对应的缩放比例就是特征值。

特征向量的物理意义

特征向量代表的是在线性变换中保持方向不变的向量。在物理学中，这可以类比为刚体的旋转或者拉伸，其中特征值对应于拉伸的比例，特征向量对应于拉伸的方向。

求解特征值和特征向量

求解特征值和特征向量的过程涉及到特征方程的建立和求解。对于矩阵oxed{A}，特征方程由oxed{det(A – λI) = 0}给出。

特征方程的建立

特征方程的建立基于行列式的性质，即当oxed{λ}取特征值时，oxed{A – λI}的行列式为零。

det[A - λI] = 0

求解特征值

通过求解特征方程，我们可以得到矩阵的特征值。对于每个特征值，我们可以进一步求解对应的特征向量。

特征值和特征向量的实际应用

特征值和特征向量在多个领域都有广泛的应用，包括但不限于图像处理、数据分析、量子力学等。

图像处理中的应用

在图像处理中，特征值和特征向量可以用于图像压缩和特征提取，从而实现图像的高效存储和识别。

数据分析中的应用

在数据分析中，特征值和特征向量是主成分分析（PCA）的基础，用于数据降维和特征提取。

特征值的计算示例

考虑一个2×2矩阵oxed{A}，我们将计算其特征值和特征向量。

A = [3 1; 1 3]

步骤一：建立特征方程

det[A - λI] = (3-λ)(3-λ) - 1*1 = λ^2 - 6λ + 8 = 0

步骤二：求解特征值

解上述方程，我们得到特征值oxed{λ1 = 4}和oxed{λ2 = 2}。

步骤三：求解特征向量

对于每个特征值，我们求解对应的特征向量。以oxed{λ1 = 4}为例，我们有：

(A - 4I)v = 0

解这个方程组，我们得到特征向量oxed{v1 = [1, 1]T}。

特征值和特征向量的FAQ

FAQ

问：特征值和特征向量在实际中有哪些应用？
- 答：特征值和特征向量在图像处理、数据分析、量子力学等多个领域都有广泛应用。在图像处理中，它们可以用于图像压缩和特征提取；在数据分析中，它们是主成分分析（PCA）的基础，用于数据降维和特征提取。
问：如何计算一个矩阵的特征值和特征向量？
- 答：首先，为给定的方阵建立特征方程oxed{det(A – λI) = 0}。然后，求解这个方程得到特征值。对于每个特征值，将其代入oxed{(A – λI)v = 0}中求解对应的特征向量。
问：特征值和特征向量在物理学中的意义是什么？
- 答：在物理学中，特征值和特征向量可以类比为刚体的旋转或拉伸。特征值对应于拉伸的比例，特征向量对应于拉伸的方向。
问：特征向量是否一定存在？
- 答：对于矩阵的每个特征值，都存在至少一个特征向量。这是因为特征向量定义为满足oxed{Av = λv}的非零向量，而特征方程的解保证了特征值的存在，从而也保证了特征向量的存在。
问：特征值可以是负数或复数吗？
- 答：是的，特征值可以是负数或复数。实际上，特征值可以是任何标量，包括零、负数或复数。特征值的性质取决于矩阵的性质和特征方程的解。