相关系数分析:深度解析
相关系数分析:深度解析
相关系数分析是统计学中用来衡量变量之间关系的一种重要方法。无论是在学术研究还是商业分析中,相关系数分析都有着广泛的应用,它不仅能够帮助研究者理解变量之间的潜在联系,还能为决策提供数据支持。
1:相关性分析的重要性
在数据分析的过程中,理解变量之间的关系是至关重要的。相关性分析通过量化的方式揭示变量之间的关系强度和方向。例如,在市场营销中,了解广告支出与销售额之间的相关性可以帮助企业优化资源配置。通过相关性系数,我们可以判断变量之间是否存在线性关系,从而在数据驱动的环境中做出更为精确的决策。
2:皮尔逊相关系数(Pearson Correlation Coefficient)
皮尔逊相关系数是最常用的相关性指标之一,其主要用于衡量两个连续变量间的线性关系。它的取值范围在-1到1之间,其中1表示完全正相关,-1表示完全负相关,0表示无相关性。皮尔逊相关系数的计算基于协方差和标准差,适用于假定数据呈正态分布的连续型数据。
-
公式说明:
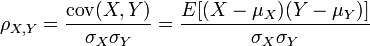
公式中,cov(X, Y)是X和Y的协方差,σX是X的标准差,μX是X的期望。 -
代码示例:
a <- c(1, 2, 3) b <- c(11, 12, 14) cor.test(a, b, method="pearson") -
图示:为了形象化地理解皮尔逊相关系数,我们通常会使用散点图来展示数据点的分布。
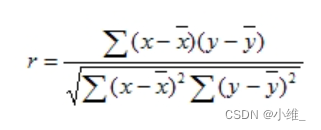
3:斯皮尔曼相关系数(Spearman Rank Correlation Coefficient)
斯皮尔曼相关系数是一种非参数的相关性分析方法,适用于对数据的等级顺序进行分析。与皮尔逊相关系数不同,斯皮尔曼相关系数不需要数据呈正态分布,因而更适合于处理偏态数据或有序数据。
-
公式说明:斯皮尔曼相关系数的计算方式类似于皮尔逊相关系数,只需要将原始数据替换为排名数据。
-
代码示例:
a <- c(1, 10, 100, 101) b <- c(21, 10, 15, 13) cor.test(a, b, method="spearman") -
应用场景:斯皮尔曼相关系数广泛应用于非线性关系的检测,如在教育领域分析学生成绩排名之间的相关性。
4:肯德尔相关系数(Kendall’s Tau Correlation Coefficient)
肯德尔相关系数用于衡量两个变量之间的排序一致性。它通过计算和谐对与不和谐对的数量差,来判断变量之间的相关性。
-
公式说明:
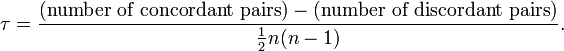
-
代码示例:
a <- c(1, 2, 3) b <- c(1, 3, 2) cor.test(a, b, method="kendall") -
应用场景:适用于小样本数据和存在重复值的情况,常用于社会科学研究中。
5:多变量相关性分析
多变量相关性分析用于研究多个变量之间的关系。主成分分析(PCA)和因子分析是其中的常见方法,主要用于降维和识别主要相关性模式。
- PCA示例:通过PCA可以将高维数据降维,保留主要信息,有助于数据可视化和模型构建。
6:相关性分析在数据科学中的应用
在数据科学中,相关性分析是数据清洗和特征选择的重要工具。它帮助数据科学家识别重要变量、消除多重共线性,提高模型的预测能力。
7:结论与未来展望
相关性分析为我们提供了一个强大的工具,可以帮助理解复杂数据集中的变量关系。随着数据量和复杂性的增加,相关性分析将在大数据分析、机器学习和人工智能领域发挥更重要的作用。通过不断发展和深化这些分析方法,我们将能够从数据中获取更丰富的洞察。
FAQ
-
问:相关系数的取值范围是什么?
- 答:相关系数的取值范围是-1到1。其中,1表示完全正相关,-1表示完全负相关,0表示无相关性。
-
问:如何选择合适的相关系数分析方法?
- 答:选择相关系数分析方法主要取决于数据的类型和分布。皮尔逊相关系数适用于正态分布的连续数据,斯皮尔曼和肯德尔相关系数适用于非正态分布或有序数据。
-
问:相关性分析与因果关系有何不同?
- 答:相关性分析仅揭示变量之间的关系强度和方向,并不表示因果关系。因果关系需要通过实验设计和因果推断来验证。
热门API
- 1. AI文本生成
- 2. AI图片生成_文生图
- 3. AI图片生成_图生图
- 4. AI图像编辑
- 5. AI视频生成_文生视频
- 6. AI视频生成_图生视频
- 7. AI语音合成_文生语音
- 8. AI文本生成(中国)
最新文章
- 将 GraphQL 单体迁移至 Apollo Federation
- 声音即身份:声纹识别API如何改变身份验证的未来
- 国内API KEY 密钥免费的AI平台及其使用指南
- 全面解读:REST API与OpenAPI的区别、应用及最佳实践指南
- 5款强大且高效的API漏洞扫描工具推荐
- Twitter (x) API 介绍:在线使用和集成指南
- DeepSeek+ima:打造高效个人知识库,提升学习与工作效率
- API设计模式:粒度细化 vs 粒度粗化的利弊分析
- 如何实现Mock API以进行API测试 | Zuplo博客
- 解读 TaskMatrix.AI
- API协议设计的10种技术
- ComfyUI API是什么:深入探索ComfyUI的API接口与应用