時間序列分析的全面指南

時間序列分析的全面指南

時間序列是一种按时间顺序排列的数据集合，广泛应用于各个领域，例如经济学、金融、气象学等。本文将深入探讨時間序列的各个组成部分及其相关技术，帮助读者掌握時間序列分析的基本概念和应用。

概念及其重要性

時間序列是指在特定时间间隔内收集的数据点，这些点可以是每天的气温、股票价格、医院急诊的数量等。時間序列分析的目标是通过研究时间序列数据的特征和模式，进行预测和决策支持。这在商业、金融等领域有着重要的应用价值，例如预测销售量、优化库存管理以及评估市场趋势。

時間序列的组成部分

趋势

趋势是时间序列中长期变化的方向，可能是上升、下降或平稳。识别趋势有助于理解数据的整体走向。图示如下：

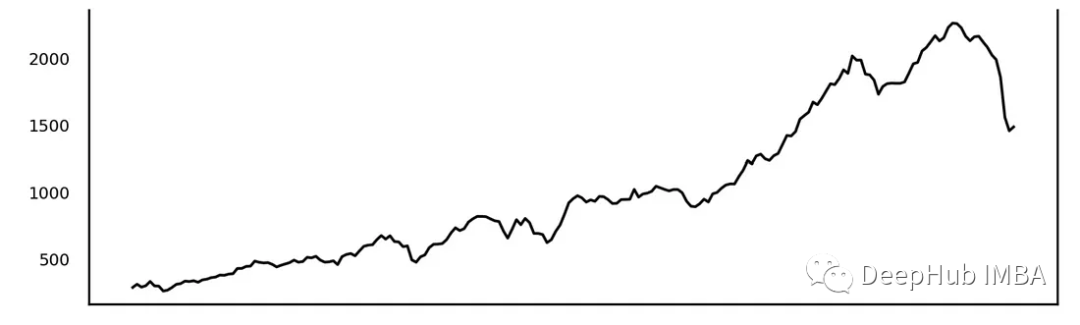
季节性

季节性指的是在固定时间间隔内重复出现的模式。识别季节性有助于预测周期性的变化，例如每年的气温波动。

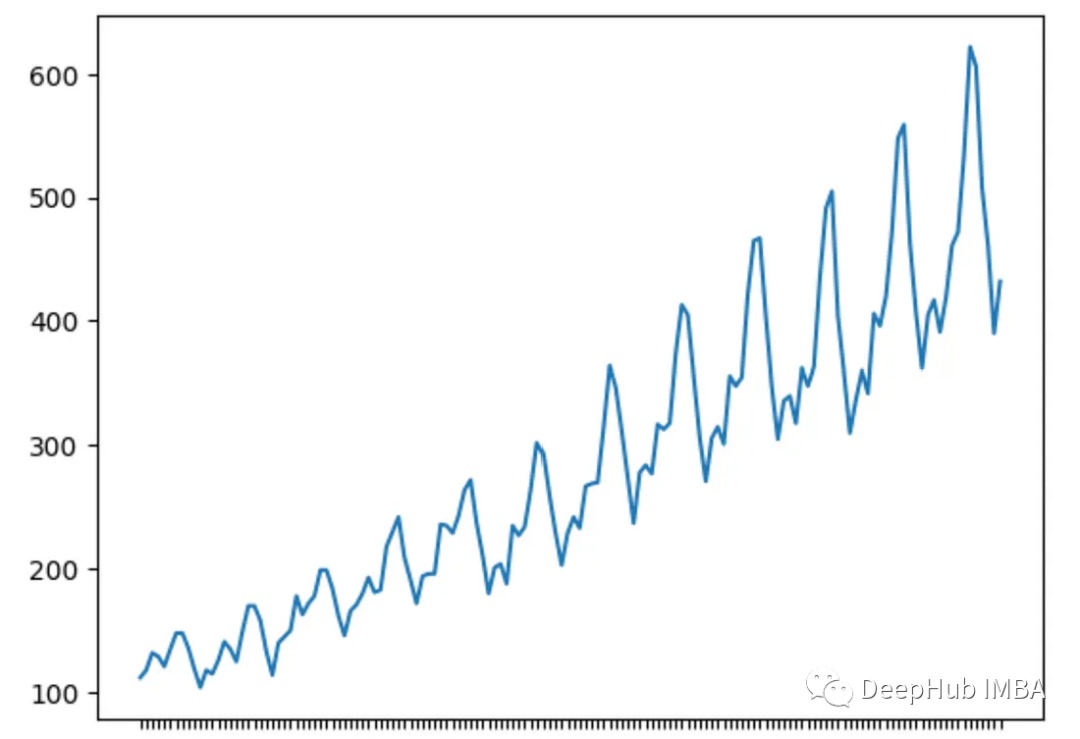
残差或白噪声

残差是时间序列中无法用趋势或季节性解释的随机性，通常被视为白噪声。理解残差有助于评估模型的预测误差。

時間序列分解与预测

時間序列分解

時間序列分解是将序列分解为趋势、季节性和残差的过程。可以使用统计工具如 statsmodels 库中的 STL 函数来实现。

import pandas as pd 
import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import STL

df = pd.read_csv('time-series-data.csv')
decomposition = STL(df['x'], period=12).fit()

分解后的时间序列可以帮助我们更好地理解数据中每个组成部分的影响。

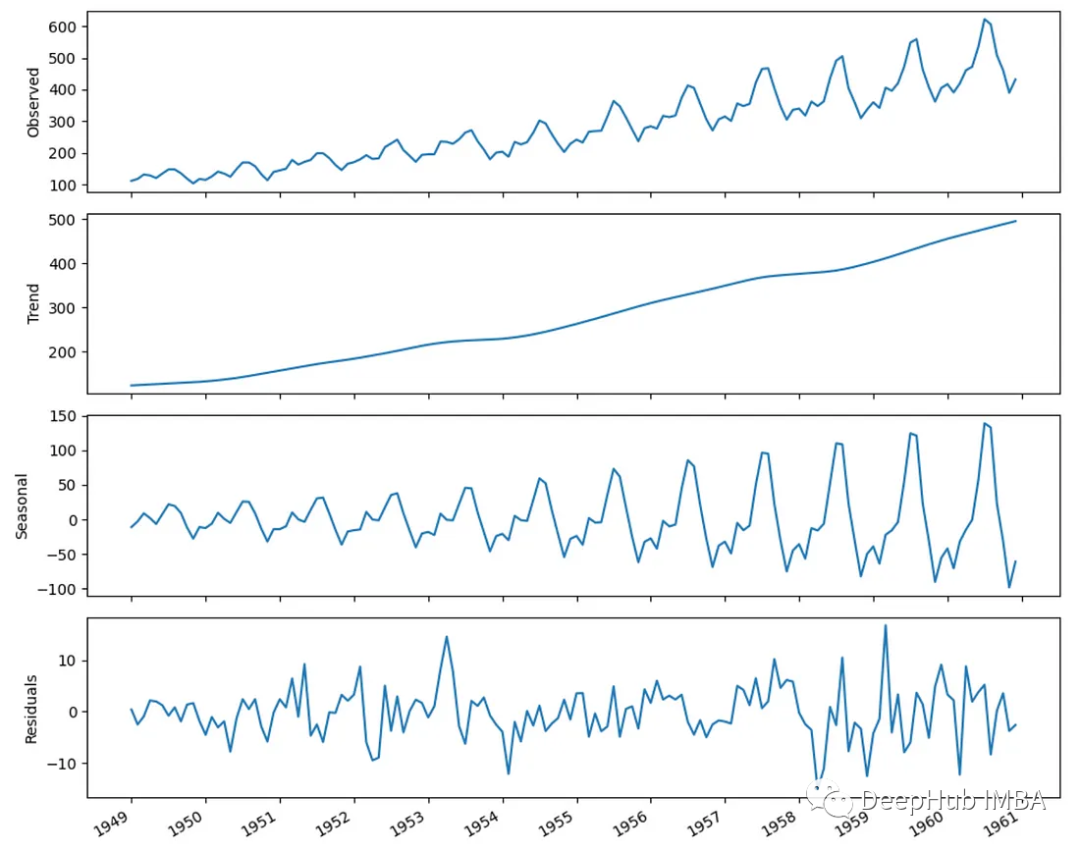
時間序列预测

预测是一种利用历史数据来推测未来数据点的技术，经常使用的模型包括自回归模型（AR）、移动平均模型（MA）、自回归移动平均模型（ARMA）等。对于复杂的数据集，深度学习模型如长短期记忆网络（LSTM）也可以用于时间序列预测。

预测模型的基本步骤

1. 收集数据：收集时间序列数据，并确保数据质量。
2. 开发预测模型：基于历史数据，选择合适的模型进行训练。
3. 部署模型：将训练好的模型应用于实际场景。
4. 模型评估与调整：监控模型性能，进行必要的调整和重新训练。

平稳性与变换

平稳性

平稳性是时间序列的一个重要属性，指序列的统计特征（如均值和方差）不随时间变化。平稳序列对于许多统计预测模型来说是理想的，因为这些模型通常假设数据是平稳的。

变换

为了获得平稳序列，常用的方法包括差分、对数变换等。这些方法可以帮助减小数据中的波动，使其更适合模型构建。

自相关与偏自相关

自相关

自相关是指时间序列中不同时间点之间的线性关系，通常通过自相关函数（ACF）图来分析。

from statsmodels.graphics.tsaplots import plot_acf

plot_acf(time_series, lags=20)

偏自相关

偏自相关是指消除较短滞后影响后，某一滞后期的自相关程度。偏自相关函数（PACF）图可以帮助确定模型中自回归项的个数。

平滑方法

平滑方法用于减少数据中的随机噪声，以便更好地观察趋势和季节性。常见的方法有移动平均法、指数平滑法等。

時間序列数据特征

静态时间序列

静态时间序列假设数据在时间上的特征不变，常用于平均数模型和指数平滑模型。

动态时间序列

动态时间序列考虑数据随时间的变化，常用于ARIMA和VAR等模型。

FAQ

1. 问：什么是时间序列分析的主要步骤？

   • 答：时间序列分析主要包括数据收集、数据预处理、特征分析、模型选择、模型训练和模型评估。

2. 问：如何判断一个时间序列是否平稳？

   • 答：可以通过绘制序列图、计算ADF检验等方法来判断时间序列的平稳性。

3. 问：什么是自相关图？

   • 答：自相关图是一种用于显示时间序列中不同时间点间相关性的工具，帮助识别序列中的模式和规律。

时间序列分析是一个复杂而重要的领域，掌握其基本概念和技术不仅有助于学术研究，也能在商业应用中发挥重大作用。