GNN中的消息传递框架与二相图的全面解析

在图神经网络（GNN）中，消息传递范式是一个核心概念，它通过聚合邻接节点的信息更新中心节点的信息。该框架不仅在学术界广受关注，也在工业界获得了广泛应用。在本文中，我们将深入探讨GNN中的消息传递框架，特别是它在二相图中的应用。

二相图在GNN中的重要性

二相图，也称为二分图，是一种特殊的图结构，其中的节点集可以分为两个不相交的子集，且只有不同子集的节点之间存在边连接。这种结构在图神经网络中具有重要的应用价值。二相图的结构使得消息传递过程更加高效，因为可以通过分离节点进行并行处理，提高计算效率。

在GNN中，二相图的应用可以简化复杂的图结构，尤其是在处理大规模数据时。通过将节点分成两类，消息传递可以在这两类节点之间进行，而无需考虑同一类节点之间的连接。这种特性使得二相图成为大型网络分析中的理想选择。

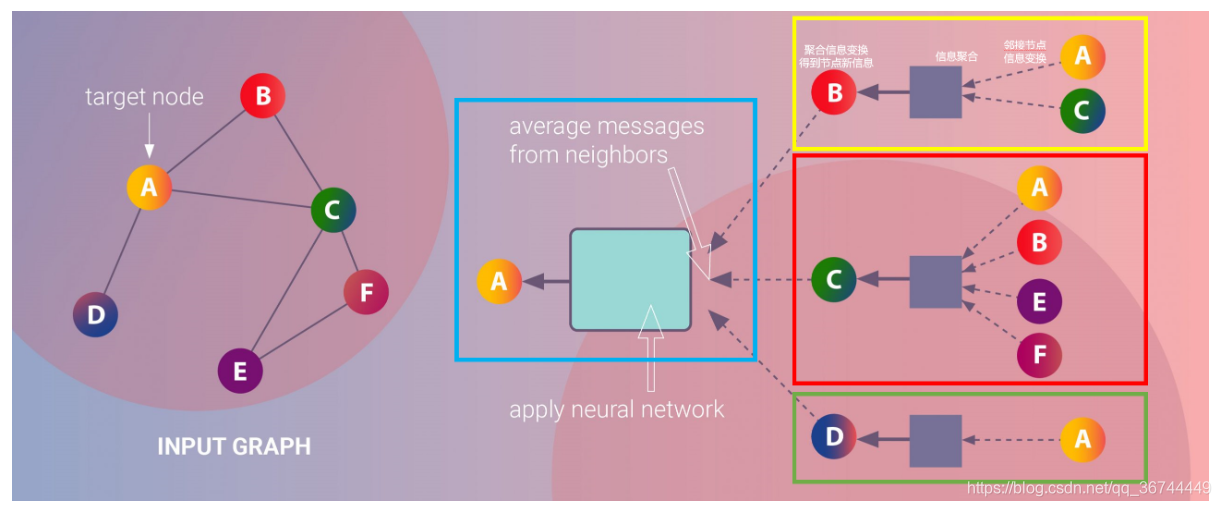
二相图示例

消息传递框架的核心步骤

消息传递框架一般包括三个核心步骤：

邻接节点信息变换：首先对邻接节点的信息进行变换，这一步通常涉及到线性变换或者非线性激活函数。
邻接节点信息聚合到中心节点：将变换后的邻接节点信息聚合到中心节点，这一步可以通过加权求和、平均或者最大值等方法实现。
聚合信息变换：对聚合后的信息进行进一步的变换，最终更新中心节点的信息。

这种范式的优点在于它的通用性和可扩展性，几乎可以应用于任何类型的图结构，尤其是在复杂的网络中，其效率和准确性都表现得尤为突出。

`MessagePassing`基类的功能

MessagePassing是Pytorch Geometric库中一个关键的基类，提供了构建基于消息传递的图神经网络的便利。通过继承这个基类，开发者可以轻松实现自定义的GNN模型。该基类封装了消息传递的基本流程，并允许用户定义消息的生成和更新方式。

在实现一个图神经网络时，开发者需要重写三个关键方法：message()、aggregate()和update()。这些方法分别用于定义消息的生成、聚合以及节点信息的更新。

import torch
from torch_geometric.nn import MessagePassing

class CustomGNN(MessagePassing):
    def __init__(self, in_channels, out_channels):
        super(CustomGNN, self).__init__(aggr='add')
        self.lin = torch.nn.Linear(in_channels, out_channels)

    def forward(self, x, edge_index):
        x = self.lin(x)
        return self.propagate(edge_index, x=x)

    def message(self, x_j):
        return x_j

    def update(self, aggr_out):
        return aggr_out

如何在GNN中实现二相图

利用MessagePassing基类，我们可以轻松实现二相图的消息传递。二相图中的节点可以分成两类，消息传递时只在这两类节点之间进行，而不会在同类节点之间传递信息。

在二相图中聚合节点信息

在二相图中，消息传递的聚合步骤只涉及不同类的节点。这意味着我们可以在聚合时利用二相图的结构特点，减少不必要的计算，提高效率。

class BipartiteGNN(MessagePassing):
    def __init__(self, in_channels, out_channels):
        super(BipartiteGNN, self).__init__(aggr='add')
        self.lin = torch.nn.Linear(in_channels, out_channels)

    def forward(self, x, edge_index):
        x = self.lin(x)
        return self.propagate(edge_index, x=x)

    def message(self, x_j):
        return x_j

    def update(self, aggr_out):
        return aggr_out

消息传递的数学表述

消息传递的数学表述通常用来描述节点信息在图中的传播过程。假设节点$i$的表示为$x_i^{(k)}$，那么经过$k$次消息传递后，节点$i$的表示更新为：

$$x_i^{(k+1)} = ext{AGGREGATE}( ext{MESSAGE}(xj^{(k)}, e{ij}))$$

其中，$ ext{MESSAGE}$函数用于生成消息，$ ext{AGGREGATE}$函数用于聚合消息。消息传递的核心在于通过图中的邻接关系，不断更新节点的表示。

图神经网络中的自环

在图神经网络的实现中，自环是一个常见的技巧。通过在邻接矩阵中添加自环，节点的信息可以在消息传递过程中保留其原始特征，从而增强模型的表达能力。

自环的实现可以通过torch_geometric.utils.add_self_loops函数实现，该函数会自动在邻接矩阵中添加自环。

自环示意图

FAQ

什么是GNN中的消息传递？
- 消息传递是一种通过聚合邻接节点信息更新中心节点信息的范式，在GNN中用于生成节点的表示。
为什么二相图在GNN中重要？
- 二相图的结构特点使得消息传递过程更为高效，特别是在处理大规模图数据时。
如何在GNN中实现自环？
- 自环可以通过torch_geometric.utils.add_self_loops函数实现，以增强节点的特征表达能力。
MessagePassing基类的作用是什么？
- MessagePassing基类提供了构建GNN的基本框架，用户可以通过继承该类实现自定义的消息传递逻辑。
在GNN中如何定义消息和聚合逻辑？
- 用户需要在MessagePassing的子类中重写message()和aggregate()方法，以定义消息生成和聚合的具体逻辑。