向量的全面解析与应用

向量在数学和物理学中扮演着重要角色，既是描述空间位置的工具，也是分析线性代数问题的基础。本文将通过对向量的定义、性质、运算和应用进行详细讲解，并结合图片和代码块进行生动展示。以下是本次探讨的主要内容：

1. 向量的基本定义与表示

向量是一种具有大小和方向的数学实体，通常用带箭头的线段表示。在数学上，向量可以看作是一组有序的实数集合。比如，二维空间中的向量可以表示为 ((x_1, x_2))，而在三维空间中则扩展为 ((x_1, x_2, x_3))。

1.1 向量的数学表示

向量在数学中通常用粗体字母表示，如 a、b，或在字母上方加箭头 (overrightarrow{a})。在计算中，向量也可以表示为矩阵形式，如：

begin{bmatrix}
x_1\x_2\ vdots \x_n
end{bmatrix}

这种表示法便于在进行矩阵运算时的应用。下图展示了二维向量的直观表示：

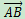
二维向量表示

1.2 向量的几何意义

在几何上，向量不仅仅是一个点到另一个点的距离，而是一个从起点到终点的方向和距离的组合。其大小（或长度）称为模，方向则由线段的方向决定。

2. 向量的模与单位向量

向量的模是指向量的长度，用于描述向量的大小。模的计算方式为向量各分量平方和的平方根。例如，一个向量 a = ((x_1, x_2))，其模为 (sqrt{x_1^2 + x_2^2})。

2.1 单位向量

单位向量是模为1的向量，用于表示方向而不考虑大小。通过将一个非零向量除以其模，可以得到对应的单位向量。单位向量在直角坐标系中的例子：

单位向量

2.2 零向量

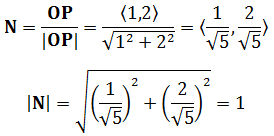
零向量是所有分量均为零的向量，表示没有方向和大小。它在向量加法中起着类似于数字零在数值加法中的作用。

3. 向量的运算

向量的运算包括加法、减法和数乘，这些运算是线性代数的基础。

3.1 向量加法

向量加法遵循平行四边形法则，即两个向量的和是由起点到两个向量终点构成的平行四边形的对角线。具体表示为：

overrightarrow{a} + overrightarrow{b} = (a_1 + b_1, a_2 + b_2)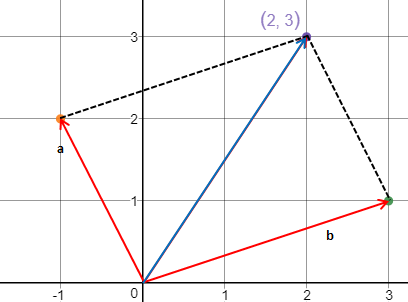

向量加法

3.2 向量的数乘

向量数乘是将向量的每个分量乘以一个标量，这会改变向量的大小而不改变方向（若标量为正）。若标量为负，则反向。

3.3 向量的减法

向量的减法可视作加上一个负向量，即 (overrightarrow{a} – overrightarrow{b} = overrightarrow{a} + (-overrightarrow{b}))。

4. 向量在直角坐标系中的应用

在直角坐标系中，向量可以用来描述空间中的位置和方向。通过将向量的起点选为坐标系原点，便可以直观地表示向量。

向量直角坐标表示

5. 向量与线性方程组

向量可以用于解线性方程组，方程组的解可以看作是向量的线性组合。如下为示例方程组的向量表示：

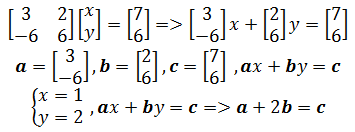
线性方程组

在几何上，这种表示可以帮助我们理解方程组解的性质和几何结构。

6. 向量在物理学中的应用

在物理学中，向量用于描述速度、力等具有方向和大小的物理量。通过向量，我们可以简化许多复杂的物理问题并进行分析。

6.1 力的合成与分解

力是物理学中常见的向量之一，多个力的合成便是向量加法的直接应用，而力的分解则是将一个力分解为多个方向上的分量。

力的合成

6.2 速度与加速度

速度和加速度同样是向量，描述物体运动的方向和速率的变化。通过向量的加减法，我们能方便地处理运动中的叠加问题。

7. 向量计算中的编程应用

在编程语言中，向量运算被广泛应用于计算机图形学、机器学习和数据分析中。通过一些简单的代码示例，我们可以直观地了解向量运算在程序中的实现。

7.1 向量加法的实现

import numpy as np

a = np.array([1, 2])
b = np.array([3, 4])
result = a + b
print(result)  # 输出: [4 6]

7.2 向量的数乘实现

scalar = 3
vector = np.array([1, 2])
result = scalar * vector
print(result)  # 输出: [3 6]

FAQ

问：向量与标量的区别是什么？
- 答：向量是具有大小和方向的数学实体，而标量只有大小没有方向。
问：如何计算一个二维向量的模？
- 答：二维向量 ((x, y)) 的模等于 (sqrt{x^2 + y^2})。
问：单位向量有何应用？
- 答：单位向量用于表示纯方向，常用于标准化其他向量。
问：如何在编程中实现向量的加法？
- 答：可以使用NumPy库中的数组进行相加，如 a + b。
问：什么是零向量？
- 答：零向量是所有分量均为零的向量，表示没有方向和大小的向量。

通过本文的详尽解析，相信您对向量的基本概念、运算及其在数学与物理中的应用有了更加深刻的理解。