二分图详解与应用

什么是二分图

二分图是图论中的一个重要概念，它的顶点集合可以被划分为两个互不相交的子集 U 和 V。在这样的图中，所有的边都连接着一个顶点在 U 和一个顶点在 V，或者反之。因此，在二分图中，任意一个子集内部的顶点之间不会存在边连接。这种特性使得二分图在图论中拥有独特的性质和应用。下图展示了一个典型的二分图：

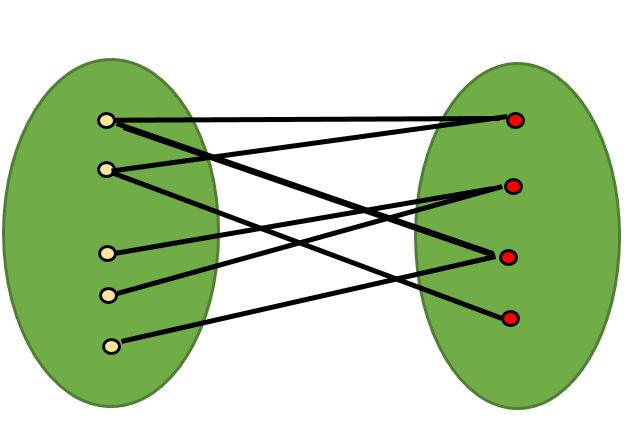
二分图示例

二分图广泛应用于匹配问题和网络流问题中，因为它的特殊结构使得这些问题的求解更为简单和高效。

二分图的判定方法

在实际应用中，我们需要判定一个给定的图是否为二分图。可以通过染色法来实现这一点，该方法涉及给图的顶点染色，使得相邻顶点的颜色不同。如果能够成功染色，即可判定该图是二分图。以下是两个经典的算法用于染色：

使用广度优先搜索（BFS）

BFS 是一种常用的遍历算法，可以用于二分图判定。下面的代码演示了如何使用 BFS 来判定一个图是否为二分图：

class Graph:
    def __init__(self, V):
        self.V = V
        self.graph = [[0]*V for _ in range(V)]
        self.colorArr = [-1]*self.V

    def isBipartiteUtil(self, src):
        queue = []
        queue.append(src)

        while queue:
            u = queue.pop()
            if self.graph[u][u] == 1:
                return False
            for v in range(self.V):
                if self.graph[u][v] == 1 and self.colorArr[v] == -1:
                    self.colorArr[v] = 1 - self.colorArr[u]
                    queue.append(v)
                elif self.graph[u][v] == 1 and self.colorArr[v] == self.colorArr[u]:
                    return False
        return True

    def isBipartite(self):
        self.colorArr = [-1]*self.V
        for i in range(self.V):
            if self.colorArr[i] == -1:
                if not self.isBipartiteUtil(i):
                    return False
        return True

if __name__ == "__main__":
    g = Graph(4)
    g.graph = [[0, 1, 0, 1],
               [1, 0, 1, 0],
               [0, 1, 0, 1],
               [1, 0, 1, 0]]

    print("Yes" if g.isBipartite() else "No")

使用深度优先搜索（DFS）

DFS 也是判定二分图的一种有效方法。以下是代码示例：

V = 4

def colorGraph(G, color, pos, c):
    color[pos] = c
    for i in range(V):
        if G[pos][i]:
            if color[i] == -1:
                if not colorGraph(G, color, i, 1-c):
                    return False
            elif color[i] == c:
                return False
    return True

def isBipartite(G):
    color = [-1]*V
    for i in range(V):
        if color[i] == -1:
            if not colorGraph(G, color, i, 1):
                return False
    return True

if __name__ == "__main__":
    G = [[0, 1, 0, 1],
         [1, 0, 1, 0],
         [0, 1, 0, 1],
         [1, 0, 1, 0]]

    print("Yes" if isBipartite(G) else "No")

二分图的应用

二分图的一大应用是求解二分匹配问题。二分匹配是选择二分图中的一组边，使得没有两个边共享同一个顶点，且边的数量尽可能多。这个问题可以通过最大流算法来解决。

最大匹配问题

在二分图中，最大匹配是指能够选择的最多不共享顶点的边的集合。最大匹配问题可以通过转化为最大流问题来求解。下图展示了匹配问题的一个应用场景：

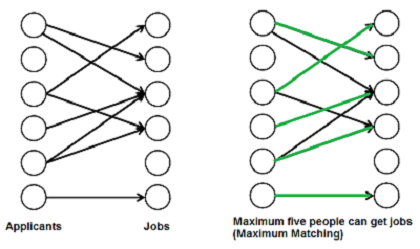
最大匹配示例

匈牙利算法

匈牙利算法是一种用来寻找二分图最大匹配的经典算法。它通过寻找增广路径来增加匹配数，具体的实现如下：

int n;      // n表示点数
int h[N], e[M], ne[M], idx;     // 邻接表存储所有边
int match[N];       // 存储每个点当前匹配的点
bool st[N];     // 表示每个点是否已经被遍历过

bool find(int x) //判断增广路径
{
    for (int i = h[x]; ~i; i = ne[i])
    {
        int j = e[i];
        if (!st[j])
        {
            st[j] = true;
            if (match[j] == 0 || find(match[j]))
            {
                match[j] = x;
                return true;
            }
        }
    }
    return false;
}

// 求最大匹配数
int res = 0;
for (int i = 0; i < n; i ++ )
{
    memset(st, false, sizeof st);
    if (find(i)) res ++ ;
}

二分图的性质

不存在奇环

二分图的一个重要性质是其内部不存在奇数长度的环。这是因为在二分图中，任何一条路径都必须从一个集合切换到另一个集合，因此所有的环都是偶数长度。这一性质可以用于快速判定一个图是否为二分图。

完全二分图

完全二分图是指在二分图中，U 中的每个顶点都与 V 中的每个顶点相连形成的图。完全二分图在很多组合优化问题中都有应用。

二分图与网络流

二分图的最大匹配问题可以通过网络流技术来解决。网络流问题是一种经典的优化问题，旨在通过网络传输最大流量。通过将二分图的匹配问题转化为网络流问题，我们可以利用现有的最大流算法来求解。

结论

二分图是图论中的基础概念之一，具有广泛的应用。无论是在理论研究中，还是在实际应用中，二分图都扮演着重要的角色。通过学习二分图的定义、性质及判定方法，我们可以更好地理解其在计算机科学中的作用。

FAQ

问：如何判断一个图是否为二分图？
- 答：可以通过染色法使用 BFS 或 DFS 遍历图，如果能将图染成两种颜色且相邻顶点颜色不同，则图为二分图。
问：什么是二分图的最大匹配？
- 答：二分图的最大匹配是指在图中选择最多的边，使得没有两个边共享同一个顶点。
问：二分图在实际中有哪些应用？
- 答：二分图广泛应用于匹配问题，如工作分配、任务调度等场景，也常用于解决网络流问题。