混合线性模型在数据分析中的应用

背景与必要性

混合线性模型（Linear Mixed Model, LMM）在现代数据分析中扮演着重要角色。它不仅是线性模型的延伸，更是处理数据相关性的重要工具。在许多研究中，数据点之间往往存在某种程度的相关性，这使得传统的线性模型难以满足独立性假设。混合线性模型通过引入固定效应和随机效应，解决了这一难题。

线性模型的假设与限制

线性模型的应用需要满足三个基本假设：正态性、独立性和同方差性。正态性要求因变量y符合正态分布；独立性要求不同类别y的观察值相互独立；同方差性则要求不同类别y的方差相等。然而，在实际应用中，这些假设往往难以同时满足。例如，在研究小镇上不同街区的居民收入与教育水平时，同一街区内的居民数据可能存在相关性，违反了独立性假设。

混合线性模型的优势

混合线性模型通过引入随机效应，允许样本之间存在相关性，从而突破了线性模型的局限。以基因表达量与采样距离相关性研究为例，混合线性模型可以有效处理由于同一患者样本之间的相关性。这不仅提高了模型的准确性，还扩大了模型的适用范围。

数据准备过程

在使用混合线性模型进行分析前，数据准备是一个关键步骤。以下是一个基于R语言的示例代码，展示如何下载和处理GEO数据：

library(GEOquery)
gset <- getGEO('GSE90627', destdir="./raw-data/",
               AnnotGPL = F,     ## 注释文件
               getGPL = F) 
gpl <- getGEO("GPL17077",destdir="./raw-data/")
ids <- Table(gpl)
a=gset1
expr=exprs(a) 
rownames(expr) <- ids[match(rownames(expr),ids$ID),7] 
pd=pData(a) 
pd <- pd[,c(1,2,37:40)]
colnames(pd)[3:6] <- c("age","gender","patient","tissue")
library(stringr)
pd$distance <- str_split(pd$title,"_",simplify = T)[,2]
pd$distance[97:128] <- rep("0cm",32)
pd$patient <- str_split(pd$title,"_",simplify = T)[,3]
pd$patient[97:128] <- str_split(pd$title[97:128],"_",simplify = T)[,2]
str(pd) #查看数据结构
save(expr,pd,file = "./Rdata/GSE90627_eSet.Rdata")

通过上述代码，用户可以将数据从公共数据库中获取，并进行初步的处理，以便进行后续的分析。

数据处理

建立混合线性模型

在混合线性模型中，固定效应和随机效应的选择至关重要。固定效应用于描述我们感兴趣的变量，而随机效应用于控制可能影响结果的其他因素。以下是一个使用R语言建立混合线性模型的示例：

df <- data.frame(CXCL1=expr["CXCL1",],pd[,c(5,7,8)])
library(lme4)
lmer.fit <- lmer(CXCL1~distance2+(distance2|patient),data = df)
summary(lmer.fit)

通过这个模型，我们可以分析基因“CXCL1”的表达量与距离的相关性。模型结果显示了固定效应和随机效应的估计值以及它们对因变量的影响。

模型可视化与解释

模型的可视化是理解结果的重要步骤。通过可视化，我们可以直观地观察到变量之间的关系和模型拟合的效果。以下代码展示了如何使用R语言对模型结果进行可视化：

library(ggeffects) 
library(ggplot2)
pred.mm <- ggpredict(lmer.fit, terms = c("distance2")) 

ggplot(pred.mm) + 
  geom_point(data = df,aes(x = distance2, y = CXCL1, colour = distance),position = "jitter") + 
  geom_line(aes(x = x, y = predicted)) +          # slope
  geom_ribbon(aes(x = x, ymin = predicted - std.error, ymax = predicted + std.error),
              fill = "lightgrey", alpha = 0.5) + # error band
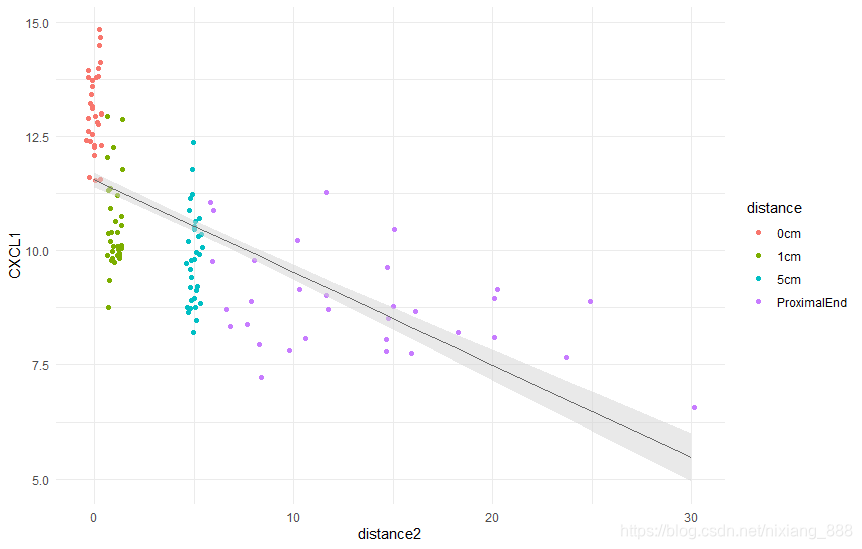
  theme_minimal()

通过可视化，我们可以清晰地看到基因表达量与采样距离之间的关系，以及模型在不同距离上的预测效果。

固定效应的显著性检验

在分析中，检验固定效应的显著性是关键的一步。通过对比包含固定效应和不包含固定效应的模型，可以判断固定效应对模型的贡献。以下代码展示了如何在R语言中进行显著性检验：

fit.full <- lmer(CXCL1~distance2+(distance2|patient),data = df,REML = F)
fit.null <- lmer(CXCL1~(distance2|patient),data = df,REML = F)
anova(fit.full,fit.null,test="LRT")

通过显著性检验，我们可以确定基因表达量与距离的相关性是否具有统计学意义。

结论与展望

混合线性模型为我们提供了一种强大的工具，用于处理数据中的相关性问题。通过合理地选择固定效应和随机效应，研究人员可以从复杂的数据集中提取有价值的信息。未来，随着数据量的增加和计算能力的提升，混合线性模型在各个领域的应用将更加广泛。

FAQ

问：混合线性模型与一般线性模型有什么区别？
- 答：混合线性模型在一般线性模型的基础上引入了随机效应，可以处理数据中的相关性问题，而一般线性模型则要求数据独立。
问：何时应该使用混合线性模型？
- 答：当数据中存在相关性或不同层次的嵌套结构时，混合线性模型是一个合适的选择。
问：如何在R语言中实现混合线性模型？
- 答：可以使用R语言中的lme4包，通过lmer函数来构建混合线性模型。

通过本文，我们深入探讨了混合线性模型的应用与优势，并提供了详细的代码示例和分析方法，帮助研究人员更好地理解和应用这一强大的统计工具。