邻接矩阵与多阶传播在图神经网络中的应用

图神经网络（Graph Neural Networks, GNNs）在处理图结构数据时表现出色，而邻接矩阵作为图的基础表示形式，在多阶传播中扮演着关键角色。本文将深入探讨邻接矩阵在多阶传播中的应用，并结合不同的图神经网络模型进行分析。

图神经网络简介

图神经网络是一类专门用于处理图结构数据的神经网络模型。它们通过对图中节点及其邻居进行特征聚合，实现信息的传播与表征。传统的GNN模型通常只在邻居层级上聚合信息，但在多阶传播中，信息可以在图中更远的范围内传播。

邻接矩阵的定义与性质

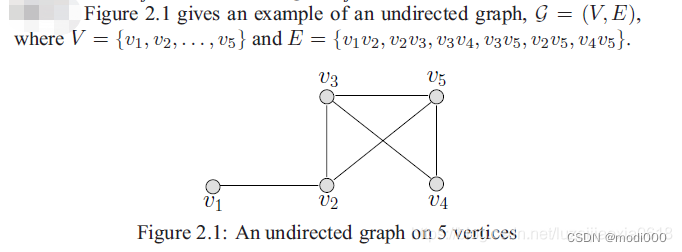
邻接矩阵是图论中的基本概念，用于表示图中顶点之间的连接关系。对于一个图G = (V, E)，其中V是顶点集，E是边集，邻接矩阵A是一个n阶方阵（n为顶点数量），其元素A[i][j]表示顶点i到顶点j之间的边关系。

无向图的邻接矩阵

• 无向图的邻接矩阵是对称的，即A[i][j] = A[j][i]。
• 主对角线上的元素通常为零，表示无自环。

有向图的邻接矩阵

• 有向图的邻接矩阵不一定对称。
• A[i][j]表示从顶点i到顶点j的边。

多阶传播的需求与挑战

在图神经网络中，多阶传播能够捕获更远距离的节点信息，提高模型的表达能力。然而，传统的单层GNN架构在进行多阶传播时，容易导致节点特征过平滑的问题。为了解决这一问题，研究人员提出了多种改进方案。

多阶传播与节点特征

• 多阶传播可以通过邻接矩阵的幂次操作实现。具体而言，邻接矩阵A的k次幂A^k能够表示节点之间的k跳关系。
• 通过累积不同阶次的邻接矩阵，可以实现多阶特征的聚合。

邻接矩阵在多阶传播中的作用

• 邻接矩阵作为信息传播的载体，直接影响着图神经网络的表现。
• 在多阶传播中，邻接矩阵的幂次操作能够帮助模型捕获更复杂的节点间关系。

Diffusion-Convolutional Neural Networks（DCNN）

DCNN是一种通过扩散卷积实现多阶传播的图神经网络模型。其核心思想是直接对每个节点采用多阶跳的矩阵进行表征，实现远程信息的聚合。

DCNN模型架构

• 特征矩阵与邻接矩阵：节点特征矩阵X与邻接矩阵A结合，计算不同阶次的转移概率矩阵P。
• 多阶聚合：通过累积不同阶次的矩阵，计算每个节点的多跳邻居信息。

class NodeClassificationDCNN(object):
    """A DCNN model for node classification.
    (K, X) -> DCNN -> Dense -> Out
    """
    def __init__(self, parameters, A):
        self.params = parameters
        self.var_K = T.tensor3('Apow')
        self.var_X = T.matrix('X')
        self.var_Y = T.imatrix('Y')
        self.l_in_k = lasagne.layers.InputLayer((None, self.params.num_hops + 1, self.params.num_nodes), input_var=self.var_K)
        self.l_in_x = lasagne.layers.InputLayer((self.params.num_nodes, self.params.num_features), input_var=self.var_X)

    def get_output_for(self, inputs, **kwargs):
        Apow = inputs[0]
        X = inputs[1]
        Apow_dot_X = T.dot(Apow, X) # 公式中P与X的相乘
        Apow_dot_X_times_W = Apow_dot_X * self.W
        out = self.nonlinearity(Apow_dot_X_times_W)
        return out

Direct multi-hop Attention based GNN（DAGCN）

DAGCN通过在注意力机制中引入多跳信息，扩展了GNN的感受野。其主要利用了Multi-hop Attention Diffusion操作，通过对多阶次的注意力进行加权，实现信息的更广泛传播。

DAGCN的多头注意力机制

• 传播注意力计算：利用LeakyReLU和tanh函数计算边的传播注意力。
• 注意力矩阵的定义：通过softmax函数规范化注意力得分。

多阶传播的效果

• 通过引入decay factor，DAGCN能够有效控制多阶传播的影响范围。
• 远处节点的attention weight会随着传播次数的增加而逐渐衰减。

图论基础：邻接矩阵与度矩阵

在分析图神经网络时，了解图论基础知识是至关重要的。邻接矩阵和度矩阵是图结构数据的基本表示方式。

度矩阵的定义

• 度矩阵是一个对角矩阵，其对角元素表示图中节点的度数。
• 在无向图中，节点的度数为与该节点相连的边的数量。

邻接矩阵与度矩阵的关系

• 邻接矩阵与度矩阵的乘积可以用于计算节点间的路径数量。
• 在有向图中，度矩阵分为出度矩阵和入度矩阵，分别表示节点的出边和入边数量。

邻接矩阵的存储与优化

在大规模图数据中，邻接矩阵的存储和计算开销是一个重要的问题。为了提高计算效率，需要对邻接矩阵进行优化。

稀疏矩阵存储

• 由于大多数图是稀疏的，邻接矩阵的非零元素很少。
• 采用稀疏矩阵存储可以有效减少存储空间和计算量。

矩阵分解技术

• 对邻接矩阵进行分解，可以提高大规模图数据的处理效率。
• 常用的分解技术包括LU分解、QR分解等。

邻接矩阵在实际应用中的案例

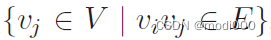
邻接矩阵在许多实际应用中扮演着重要角色，尤其是在社交网络、物流网络等领域。

社交网络分析

• 邻接矩阵用于分析社交网络中的用户关系。
• 多阶传播可以帮助识别潜在的社交群体和影响力节点。

物流网络优化

• 邻接矩阵用于表示物流网络中的运输路线。
• 通过多阶传播，可以优化运输路径，提高物流效率。

结论

邻接矩阵在多阶传播中的应用为图神经网络提供了强大的工具，能够有效捕获图中节点间的复杂关系。通过对邻接矩阵的优化和模型的改进，GNN在大规模图数据中的应用前景广阔。

FAQ

1. 问：什么是邻接矩阵？

   • 答：邻接矩阵是一种用于表示图中节点间关系的矩阵，其元素表示节点间是否存在边连接。

2. 问：多阶传播如何提高GNN的性能？

   • 答：多阶传播允许信息在更大范围内传播，能够捕获节点间更复杂的关系，从而提高模型的表达能力。

3. 问：如何优化邻接矩阵的存储？

   • 答：可以通过稀疏矩阵存储和矩阵分解技术来优化邻接矩阵的存储和计算效率。

4. 问：DCNN与传统GNN有何不同？

   • 答：DCNN通过扩散卷积实现多阶传播，能够在单层网络中捕获远程信息，而传统GNN通常需要多层结构。

5. 问：邻接矩阵在社交网络分析中的作用是什么？

   • 答：邻接矩阵用于分析用户关系，通过多阶传播可以帮助识别潜在的社交群体和影响力节点。