邻接表：高效图存储与操作的实现

在计算机科学中，图（Graph）是一种重要的数据结构，用于表示一组对象及其关系。图的存储方式通常有两种：邻接矩阵和邻接表。本文将深入探讨邻接表的实现及其在不同情况下的优势。

邻接表的概念和基本结构

邻接表是一种结合数组和链表的图存储方式。其基本思想是为每个顶点建立一个链表，链表中存储与该顶点相连的所有顶点。

顶点和边的表示

在邻接表中，顶点通常存储在一个一维数组中，而每个顶点的边信息则以链表的形式存储。链表中的每个节点表示一条边，包含目标顶点的索引和权重信息（如果有）。

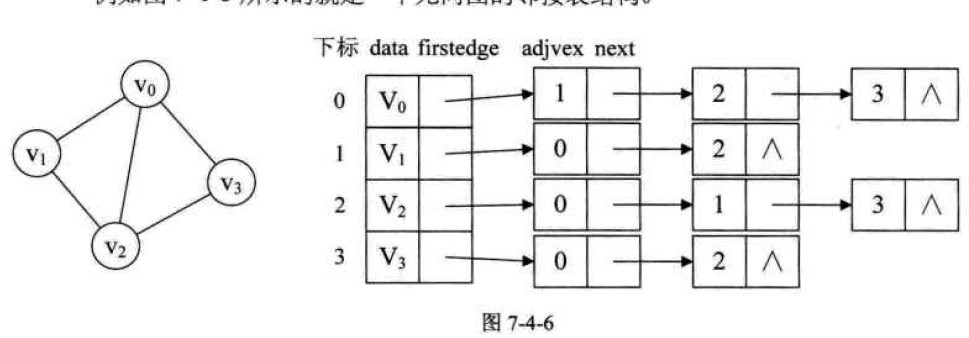
邻接表示例

有向图与无向图的区别

对于无向图，每条边在两个顶点的邻接表中都需要记录。而对于有向图，边仅在起始顶点的邻接表中记录。这样，可以有效地表示出度和入度。

有向图邻接表

邻接表的实现步骤

实现邻接表需要以下几个步骤：

1. 结构体定义

在实现邻接表时，我们首先需要定义数据结构。通常包括顶点节点和边节点。

typedef struct EdgeNode {
    int adjvex;  // 邻接点域, 存储该顶点对应的下标
    EdgeType weight;  // 权值
    struct EdgeNode *next;  // 指向下一个邻接点
} EdgeNode;

typedef struct VertexNode {
    VertexType data;  // 顶点信息
    EdgeNode *firstedge;  // 边表头指针
} VertexNode, AdjList[MAXVEX];

2. 图的创建

图的创建涉及输入顶点和边的信息，并通过头插法将边节点插入到对应的顶点链表中。

void CreateALGraph(GraphAdjList *Gp) {
    int i, j, k;
    EdgeNode *pe;
    cout << "输入顶点数和边数:" <> Gp->numNodes >> Gp->numEdges;

    for (i = 0; i numNodes; i++) {
        cout << "输入顶点信息：" <> Gp->adjList[i].data;
        Gp->adjList[i].firstedge = NULL;
    }

    for (k = 0; k numEdges; k++) {
        cout << "输入边(vi,vj)的顶点序号i,j：" <> i >> j;
        pe = (EdgeNode *)malloc(sizeof(EdgeNode));
        pe->adjvex = j;
        pe->next = Gp->adjList[i].firstedge;
        Gp->adjList[i].firstedge = pe;
    }
}

3. 邻接表的遍历

打印邻接表可以帮助我们验证数据结构是否正确。

void PrintGraph(GraphAdjList *Gp) {
    for (int i = 0; i numNodes; i++) {
        cout <adjList[i].data <adjList[i].firstedge;
        while (p) {
            cout <adjvex <next;
        }
        cout << endl;
    }
}

邻接表的优缺点

优点

节省空间：对于稀疏图，邻接表比邻接矩阵更节省空间，因为它只存储实际存在的边。
易于遍历：可以快速访问某个顶点的所有邻接点。

缺点

判定两顶点邻接关系较慢：需要遍历链表。
插入和删除操作复杂：相对于邻接矩阵，链表操作相对复杂。

邻接表的应用场景

适用于稀疏图

由于邻接表的空间效率，它非常适合用于存储稀疏图，即边的数量远小于顶点数量平方的图。

网络中的应用

邻接表在网络路由、社交网络等图表示中有广泛应用，因为这些网络通常是稀疏的。

逆邻接表

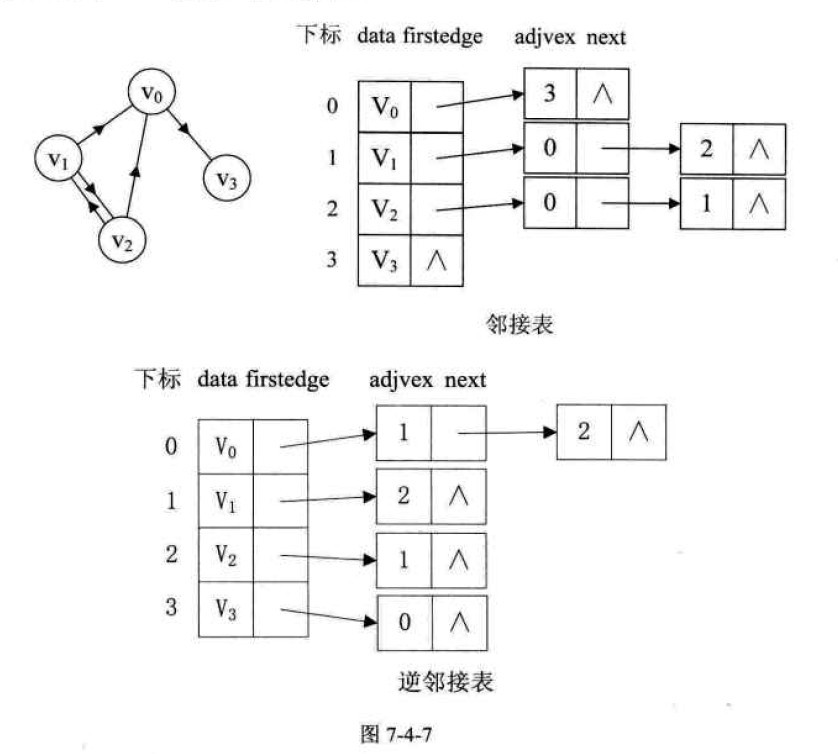
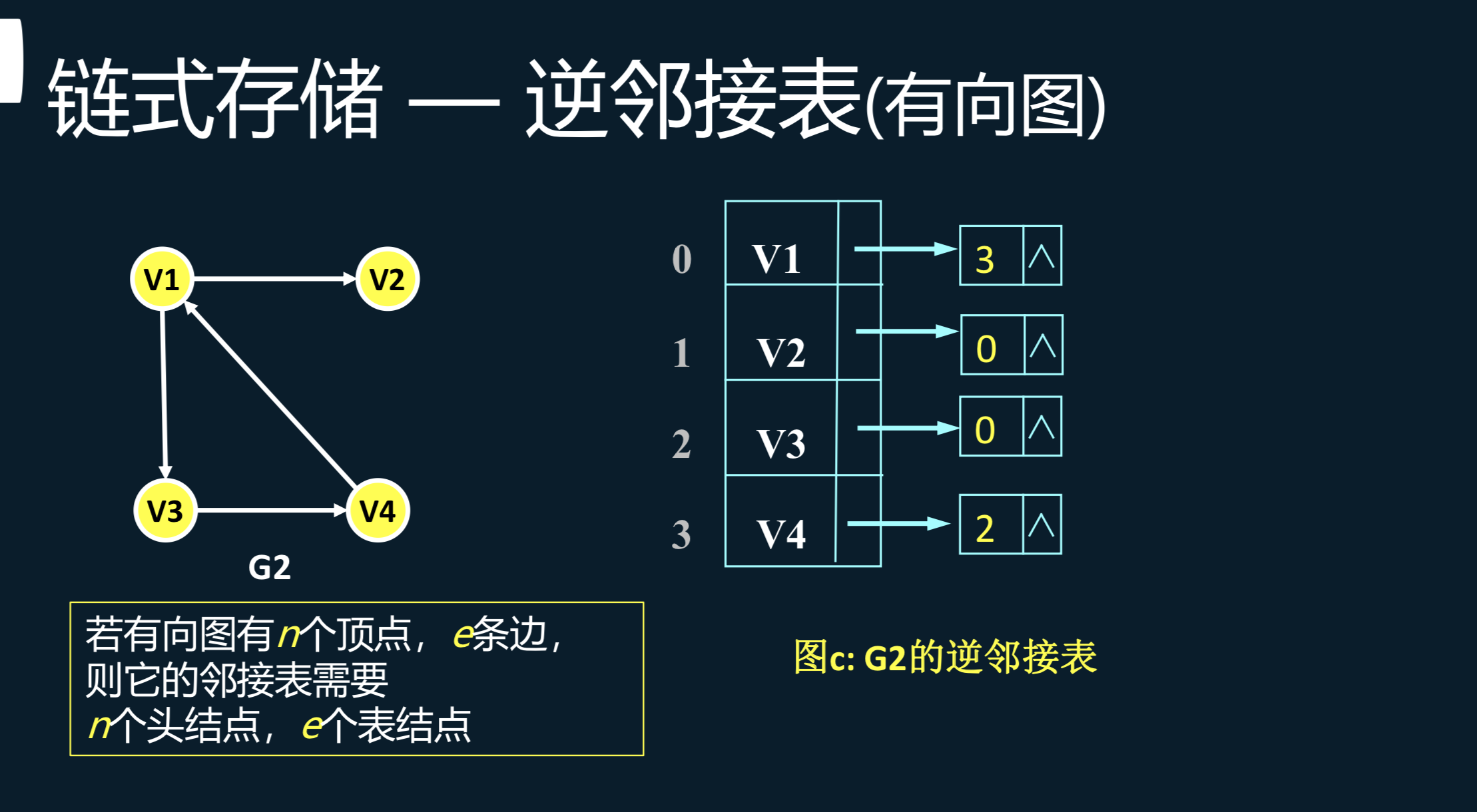
逆邻接表是邻接表的变体，记录每个顶点的入度边信息，适用于某些需要快速访问入度信息的算法。

逆邻接表示例

邻接表与邻接矩阵的比较

存储方式

邻接矩阵：使用二维数组存储顶点和边。
邻接表：使用链表存储与顶点相连的边。

操作特性

邻接矩阵：适合快速判断两顶点是否邻接。
邻接表：适合快速遍历某顶点的邻接点。

代码示例：Java实现

以下是邻接表的Java实现，展示了顶点和边的结构。

class ArcNode {
    int adjVex;//存放相邻结点的序号
    ArcNode nextArc;//下一个边结点
    int weight;//权重

    public ArcNode() {
        adjVex = 0;
        weight = 0;
        nextArc = null;
    }
}

class VNode {//顶点结点
    T data;//存储顶点的名称或其他相关信息
    ArcNode firstArc;//指向顶点Vi的第一个边结点

    public VNode() {
        data = null;
        firstArc = null;
    }
}

结论

邻接表是一种高效的图存储方式，特别适合用于处理稀疏图。通过结合数组和链表，邻接表实现了空间和时间的有效平衡。在实际应用中，根据图的稀疏程度和操作需求选择合适的存储方式。

FAQ

问：什么是邻接表？
- 答：邻接表是一种结合数组和链表的图存储方式，每个顶点对应一个链表，链表中存储与该顶点相连的边。
问：邻接表相比邻接矩阵有什么优势？
- 答：邻接表在处理稀疏图时更节省空间，因为它只存储实际存在的边，而不是所有可能的边。
问：如何判断两顶点是否邻接？
- 答：在邻接表中，需要遍历一个顶点的链表，查找是否存在与另一顶点的连接。